Thouless energy in Josephson SN-N-NS bridges

In recent years, there has been a reawakened interest in Josephson structures in which the weak coupling region exhibits a metallic type of conductivity[1-11]. These structures are anticipated to surpass the integration limitations faced by superconducting devices used in digital information processing. The steady-state properties of SNS Josephson sandwiches and superconductor/normal metal/superconductor SN-N-NS bridges have been intensively studied[10-19].

In Ref.[12] assuming the fulfillment of rigid boundary conditions at the SN interfaces, it was shown that in the case when the distance \( L \) between the S-electrodes significantly exceeds the characteristic decay length of superconducting correlations in the N-layer \( \xi=(D/2\pi T)^{1/2} \), the decay of the critical current \( I_c \) with increasing \( L \) depends significantly on the ratio between the operating temperature \( T \) and the critical temperature of the superconducting electrodes \( T_c \) (here \( D \) is the diffusion coefficient of an ordinary metal). At small temperature (\( T\ll T_c \)) there is a power dependence (\( I_{c}\propto 1/L^2 \)). With increasing temperature, the dependence of \( I_c \) on \( L \) becomes exponential: \( I_{c}\propto\exp\left(-L/\xi\right) \).

In Ref.[17] these studies were complemented by a more detailed analysis of the temperature dependence of the critical current at low temperatures \( T\ll T_c \). Numerical calculations carried out in Ref.[17] allowed the authors to propose an approximation formula for \( I_c \)

The fitting parameters \( \alpha \approx 10.82 \) and \( \beta \approx 1/3 \) correspond to the limit of small Thouless energy \( E_{T} \) as compared to the magnitude of the order parameter \( \Delta \) in S-electrodes. In the opposite limit (\( E_{T}\gg T \)) the dependence \( I_{c}(E_{T}) \) has the following form

The publication of these results[17] stimulated the study of SNS-based structures aiming to experimentally determine the Thouless energy[17, 18, 20-42]. Experimental studies have shown that the values of the parameter α in the expression (1) obtained in Ref.[17] are at least several times larger than their experimental values. As a possible reason for this discrepancy, the presence of finite transparency of the SN boundaries of the studied Josephson contacts has been hypothesized. To account for this circumstance, a renormalization of the Thouless energy was proposed[18]

Here, \( r \) is normalization coefficient, \( G_{N} \) and \( G_{B} \) are the conductance of the normal wire and the SN interface, respectively, \( A \), \( B \), and \( C \) are fitting parameters. It is important to note that the authorsof Ref.[18] ”donothavea good explanation of the factor \( r^B \) and the numerical value of \( B \)” that they used to fit the data. Additionally, the fitting coefficients \( A \), \( B \), and \( C \) are not universal. Even for a set of samples differing by the distance \( L \) between the electrodes with fixed other parameters, all these coefficients will be sample-dependent.

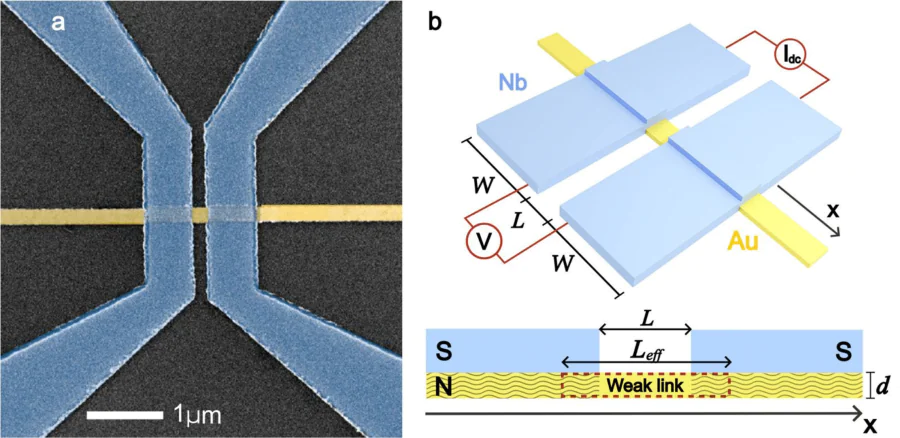
It should be noted that almost all the experimental works cited above used the shadow mask technique to fabricate SNS-based Josephson contacts. The resulting hybrid structures had the SN-N-NS bridge geometry shown in Figure 1. In this type of contact, the effective distance \( L_{\rm eff} \) between the S-electrodes is not the geometric size \( L \) of the weak bonding region. This region is delocalized (in the other words, without rigid boundaries) and includes the areas of the N-film under the superconductors where current injection into the superconductor takes place. The presence of such delocalization was also qualitatively indicated by the experimental data. Indeed, substitution of the experimentally determined \( E_{T} \) into the expression (1) gave an estimate of the size of the weak coupling region, which is larger than \( L \). In our opinion, there is a significant difference in the geometry of the SN and SN-NS interfaces that leads to an overestimation of the theoretical value of the Thouless energy calculated using rigid boundary conditions at the interface of the composite SN electrode with the N-film of the bridge. The purpose of this article is to perform a detailed analysis of the proximity effect between the SN electrode and the N-film of SN-N-NS bridge structures and to derive an expression for the Thouless energy that takes into account both the finite transparency of their SN boundaries and the delocalization of the weak link region.

Figure 1

a – Scanning electron microscope image of an Nb/Au-Au-Au/Nb bridge with superconducting Nb electrodes and an Au weak link. b – Top part: three-dimensional sketch of the Josephson superconductor/normal metal/superconductor (SN-N-NS) bridge. The sample is connected using a four-point scheme. Bottom part: side view of the Josephson SN-N-NS bridge. Wavy lines indicate the proximized region of the N-layer under the S-electrode, and the red frame indicates the effective weak link.

Before that, it is first necessary to define what we mean by the Thouless energy in Eq. (1) in the considered SN-N-NS structures. According to the definition[43-46] \( E_{T} \) characterizes the sensitivity of the energy state of the system to a modification of boundary conditions. This correlates with the existing characteristic scale of spatial changes in the system’s parameters with its geometric dimensions. Unfortunately, for SN-N-NS junctions the geometric size of the weak link region cannot be strictly determined. Moreover, a supercurrent across the junction is expressed by the sum of the terms combined by the Green’s function over the Matsubara frequencies, therefore the characteristic scale of spatial variations in the N-film \( \xi_\omega=(D/2\omega)^{1/2} \) depends on the Matsubara frequencies \( \omega=\pi T(2n+1) \), where \( n=0, 1, 2\ldots \) In the low-temperature range \( T\ll T_c \) this sum converges at \( \omega \approx \pi T_c \). Thus, there is wide range of parameters (\( L \) and \( \xi_\omega \)) with some uncertainty in the choice of a single characteristic scale for spatial changes in the structure. 

There is another interpretation of the Thouless energy. It suggests that two states whose energies differ by less than the Thouless energy are correlated. Otherwise, they can be considered as independent single-particle states whose energies are not shared. In our particular case, we are not dealing with the energy of states, but with a set of Green’s functions which determine the supercurrent. The difference in the nature of the spatial changes in these functions is determined by the Matsubara frequency \( \omega=\pi T(2n+1) \). Therefore, the interval at which the changes occur is equal to \( 2\pi T \). 

In order to determine from a numerical solution of the Usadel equations or from experimental data the temperature \( T_{Th} \) for the transition from a sharp increase to a smooth character of the current change with decreasing temperature, we can introduce the Thouless energy for our problem as \( E_T=2\pi T_{Th} \). The Thouless energy determined in this way gives us the temperature at which the structural transitions from a discrete to an integral representation of its properties, such as the order parameter and the superconducting current (supercurrent), takes place.

It should be emphasized that the definition of \( E_T=2\pi T_{Th} \) is absolutely equivalent to the standard definition of \( E_{Th} \) in Eq. (1). By introducing the Thouless energy as described above, we can further use the relation (1) to estimate the characteristic scale of spatial variations in SNS structure as \( L = (D/2\pi T_{Th})^{1/2} =\xi \) and thus find that \( L \) coincides with \( \xi_\omega \) at the first Matsubara frequency \( \omega=\pi T \) and \(  T=T_{Th}=E_{T}/2 \pi \), that is, with the maximum value among the scales \( \xi_{\omega} \). In other words, the result of the above reasoning can be reformulated as follows: the Thouless energy is indeed defined by the expression (1). The value of the Thouless temperature \( T_{Th}=E_T/2\pi \) required for processing of experimental data follows from the equality of the geometrical size of the structure with the maximum value of \( \xi_{\omega} \) among the set of characteristic scales of the problem.

Thus, according to the established rule for the Thouless energy \( E_{T} \) in the considered planar SN-N-NS structures, we have to proceed from the equality of the scale \( \xi_{\omega} \) to the effective geometric size of the weak coupling region \( L+\zeta_{\omega} \)

at the first Matsubara frequency \( \omega=E_T /2 \). Here, \( \zeta_{\omega} \) is the maximum value among characteristic scales of spatial changes in the N-layer underneath the S-films and \( \kappa \) is a parameter that fixes the part of the effective coherence length \( \zeta_{\omega} \) by which the effective distance between the electrodes increases (formal definition of \( \kappa \) is given below). Note that at \( \zeta_{\omega}=0 \) the expression (4) is transformed into the definition (1) of \( E_{T} \), which was previously used to describe SNS sandwiches with rigid boundary conditions at the SN interfaces.

To determine \( \zeta_{\omega} \) it is sufficient to solve the problem on the proximity effect between a semi-infinite N-film and an extended SN electrode.

We assume that the dirty-limit conditions are satisfied both in the superconductor and normal metal in the bridge, its SN boundaries have finite transparency, and the thickness of the N-film \( d_N \) is much less than \( \xi_N=(D/2\pi T_c)^{1/2} \). The suppression of superconductivity in the S-film due to the proximity effect with the N-layer is considered negligible and it is not taken into account. Under these assumptions the proximity effect between the semi-infinite SN electrode (at \( x\geq 0 \)) and the semi-infinite N-film (at \( x\leq 0 \)) can be considered in the framework of the Usadel equations[47]. It was shown[48] that the Usadel equation for the \( \theta \) function in the N-film under the S-electrode they can be written in the form

where

and 

\( \gamma_{BM}=\gamma_B d/\xi_N \), \( \gamma_B=R_B/\rho_N \xi_N \), \( R_B \) is the specific boundary resistance, \( \Delta \) is the absolute value of the order parameter in the S layer, which has the BCS-like temperature dependence. We conclude that

The Usadel equation in the N-film can be written as follows

The existence of the first integrals of the equations (5) and (9)

permits to get their analytical solutions 

where \( Q=\tan \frac{\theta(+0)-\theta(\infty )}{4} \)

The integration constants \( \theta(\pm0) \) in Eqs. (12)–(13)

have been determined from the boundary conditions

at SN-N interface \( (x=0) \).

Substitution of Eq. (8) into Eq. (4) at the first Matsubara frequency \( \omega= E_T /2 \) results in

where \( \epsilon=E_{T}/ 2\pi T_c \), \( \gamma^{\ast }\approx 1.781 \) is Euler’s constant. For simplicity we replace \( \Delta \) with its value \( \pi T_c/\gamma^{\ast} \) at \( T\ll T_c \). 

In the limit \( \epsilon \gamma_{BM} \gg 1 \) Eq. (16) transforms to 

Note that as \( \gamma_{BM}\rightarrow \infty \) the SN boundaries become completely non-transparent for quasiparticles in the N-region, therefore thequasiparticle current cannot flow from the N-film of the SNS contact into the S-electrodes. If the length of the SN boundaries of the composite SN electrodes of the SN-N-NS structure significantly exceeds \( \zeta_{\omega} \), the length of the current localization region in its N-part can be considered infinite. Therefore, in full agreement with Eq. (1), the parameter \( \epsilon \) should tends to zero, as \( \gamma_{BM}\rightarrow \infty \). From this requirement we get \( \kappa =1/2 \) and 

Suppose further that the parameter \( \kappa \) is independent on \( \gamma_{BM} \) in the opposite limit \( \epsilon \gamma_{BM} \ll 1 \), then we get 

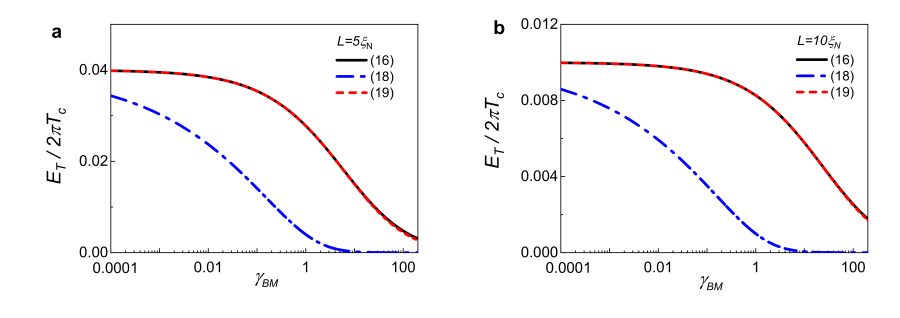
Figure 2a,b show the dependence of the Thouless energy \( E_{T} \) on the suppression parameter \( \gamma_{BM} \), calculated using equations (16), (17), and (19), for the distances between the electrodes SN-N-NS structures, which are \( L=5\xi_N \) and \( L=10\xi_N \). The calculations show that the approximation formula (19) coincides with the exact dependence \( E_{T}(\gamma_{BM}) \) calculated by the formula (16) within the specified range of parameters for long bridges. A noticeable discrepancy between the curves calculated by formulas(16) and (19) only appears in the \( \gamma_{BM}\gg 100 \) limit – this scenario is not realized in the experiments involving SN-N-NS structures.

Figure 2

a, b – Thouless energy \( E_{T} \) versus interface parameter \( \gamma_{BM} \) in the SN-N-NS bridge with the distances between the electrodes \( L=5\xi_N \) (panel a) and \( L=10\xi_N \) (panel b), calculated from the Eq. (16) (solid line) and from the asymptotic expressions (18) (dash-dotted line) and (19) (dashed line), valid in the limit of \( \epsilon \gamma_{BM} \gg 1 \) and \( \epsilon \gamma_{BM} \ll 1 \), respectively.

At the same time, the expression (17) fits the exact dependency \( E_{T} (\gamma_{BM}) \) rather poorly. The reason is that the condition \( \epsilon \gamma_{BM} \gg 1 \) is not fulfilled even in the region of large \( \gamma_{BM} \). This is due to the fact that \( \epsilon \) decreases much faster than \( \gamma_{BM}^{-1} \). The difference between the exact solution (16) and that resulting from asymptotic expression (17) becomes more obvious as \( L/\xi_N \) increases.

It is easy to see that when \( L \gg \xi_N \sqrt{\gamma_{BM}} \) the expression (16) is reduced to Eq. (1). Physically, this limit is equivalent to the fulfillment of rigid boundary conditions at the N boundaries of the bridging film with its NS electrodes. In this limit, as in the SNS sandwiches investigated in Ref.[17] the rigid boundary conditions do not impose any additional characteristic lengths characterizing the spatial variations of parameters in the N film of SNS or SN-N-NS structures. The weak coupling region turns out to be a “closed” system, characterized only by its intrinsic parameters, such as the diffusion coefficient \( D \). The Thouless energy (1) was introduced precisely for such “closed” systems.

Going beyond the rigid boundary conditions, such as considering the finite transparency of SN boundaries in SNS sandwiches or the delocalization of the weak coupling region in the studied SN-N-NS structures, violates the closure condition. Additional scales appear in the problems determined by the suppression parameter \( \gamma_B \) in SNS sandwiches or \( \gamma_{BM} \) in SN-N-NS structures. Therefore, in SN-N-NS bridges in accordance with the formula (16) at \( L \ll \xi_N\sqrt{\gamma_{BM}} \) the diffusion coefficient no longer characterizes the system and the Thouless energy \( E_T = \pi T_c/ \gamma_{BM} \) in the first approximation is determined only by the parameter \( \gamma_{BM} \), i.e., by the properties of the SN boundaries.

The proposed implicit definition (16) of \( E_{T} \) is a compromise solution, considering both the internal parameters of the N-metal in the weak coupling region and the peculiarities of induced superconducting correlations in in the N-metal.

The dependence of the superconducting current density \( I \) on the phase difference of the order parameters of the superconducting electrodes \( \varphi \) in the SN-N-NS junctions has been previously calculated by numerically in Ref.[10] for arbitrary values of \( \gamma_{BM} \) and \( L/\xi_N \). Just as in the approach we used earlier in Section II, the suppression of superconductivity in the S-film was not taken into account in Ref.[9] For computational convenience, the Usadel equations were written in the \( \Phi \) representation (the origin of the \( 0x \) axis is placed in the center of the structure)

Here, \( \Phi \) and \( G=\Omega /(\Omega ^{2}+\Phi \Phi ^{\ast })^{1/2} \) are Usadel Green’s functions, the Matsubara frequencies \( \Omega =(2n+1)T/T_{c} \) are normalized on \( \pi T_{c} \), the \( x \)-coordinate is normalized on \( \xi _{N} \), and \( I_0= T_{c}/e\xi _{n}\rho _{N} \), where \( \rho_N \) is residual resistivity of the N-film. The modulus of the order parameter in the S-electrode \( \Delta \) has the BCS-like temperature dependence and it is normalized on \( \pi T_{c} \); \( \varphi /2 \) is the phase of the order parameter for the right electrode (\( x\gtrsim L/2 \)).

Equations (20) and (21) should be supplemented by appropriate boundary conditions. At \( x=0 \) these conditions follow from the symmetry of the considered problem

At a large distance from the N-NS boundary, the function \( \Phi \) converges to a solution that is independent of \( x \)

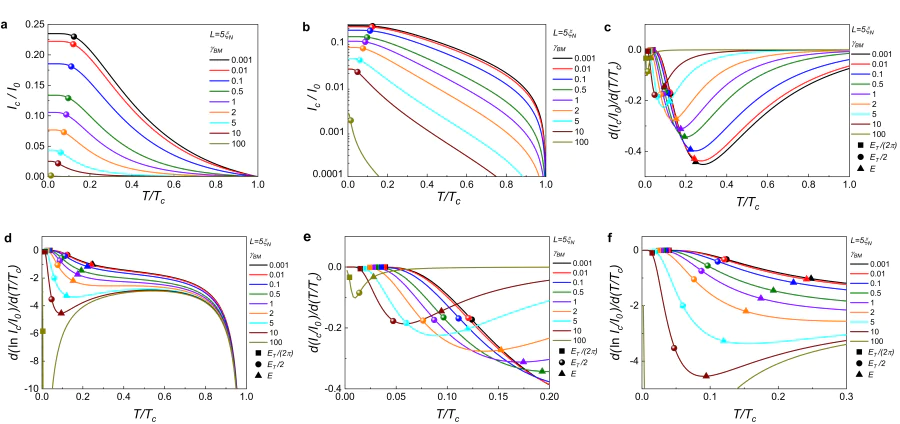
Figure 3a,b show the \( I_c(T) \) dependences calculated for \( L=5\xi_N \) and for various interface parameters \( \gamma_{BM} \) ranging from 0.01 to 100. For convenience, they are presented in linear and logarithmic scales. The points on these curves (\( \circ \)) correspond to the halfed Thouless energy (\( T/T_c = E_T/2 \)). The \( E_{T} \) values are calculated for \( L = 5 \xi_N \) and various \( \gamma_{BM} \) using Eq. (19). These figures clearly show that in the vicinity of \( E_{T}/2 \) the slope of the dependences \( I_c(T) \) changes, i.e., there is a transition from a smooth to a sharp temperature drop of \( I_c(T) \) with increasing temperature (see Figure 3a,b).

Figure 3

a, b – Temperature dependences of the critical current density \( I_c \) of the SN-N-NS bridge with \( L=5\xi \) calculated numerically for different interface parameters \( \gamma_{BM} \) in linear (panel a) and logarithmic (panel b) scales. c-f – Temperature dependences of the first derivative of the critical current density \( \frac{dI_c/I_0}{dT/T_c} \) for the same parameters in linear (panel c) and logarithmic (panel d) scales, respectively. The squares, points, and triangles on each of the calculated curves show the temperature values corresponding to \( E_T/(2\pi) \), \( E_T/2 \), and \( E_{T} \), respectively. The values of \( E_{T} \) were calculated using the expression (19) for each combination of \( \gamma_{BM} \) and \( \xi_N \) parameters. Panels e and f are enlarged versions of panels c and d in the low-temperature region.

In addition to the temperature \( T=E_T /2 \), two other characteristic temperature values can be noted. They are \( T=T_{Th}=E_T/2 \pi \) marked with squares and \( T=E_T \) marked with triangles on the temperature dependences of the first derivative of the critical current with respect to temperature (see Figure 3c-f). Figure 3d,f clearly show that for \( L=5\xi_N \) and \( \gamma_{BM}=0.01 \) the Thouless temperature is \( T_{Th}\approx 0.04 T_c \). The increase of the parameter \( \gamma_{BM} \) is accompanied by a shift of the values of this temperature towards \( T=0 \), so that at \( \gamma_{BM}=2 \), the value of \( T_{Th} \) turns out to be equal to \( \approx 0.025 T_c \). At \( T=T_{Th} \) and below the critical current reaches saturation. So the first derivative \( dI_c/dT \) is zero at \( T \lesssim T_{Th} \). From the presented in Figure 3d,f dependences it also follows that there are two extra points to be mentioned. At \( T \approx E_{T} \) and \( \gamma_{BM} < 5 \) the local minimum of the derivative is reached. At \( T \approx E_{T}/2 \) an inflection point of \( dI_c/dT \)appears for \( \gamma_{BM} < 5 \). Qualitatively, this point corresponds to the transition area between the saturation region and decreasing part of \( I_c(T) \) dependence. These reference points at \( T=E_{T}/2 \) and \( T=E_{T} \) can be useful when values of \( T=T_{Th} \) are difficult to achieve due to limitations on the temperature range allowed for measurements. In the limit \( \gamma_{BM} \gg 5  \) the effective impact of boundaries increases and the positions of the considered points \( T \approx E_{T}/2 \) and \( T \approx E_{T} \) areshifted.

Note that in the limit of a small critical current the boundary value problem (20)-(25) may also have an analytical solution. This limit is realized in the case when it is possible to neglect the suppression of anomalous Green’s functions induced in the N-film by the current flowing through it.

In the \( L\gg \xi \) limit, the superconducting state near the center of the bridge can be described by the superposition of anomalous Green’s functions (13)–(14) penetrating from the superconducting banks into the bridge (see Refs.[16, 49, 50])

where \( \theta(x) \) is the solutions of the proximity problem (12)–(14). By substituting this solution of the Usadel equations into the expression for the supercurrent [see Eq. (23)], we arrived at a sinusoidal dependence of the supercurrent on the phase difference \( \varphi \) with a critical current density equals to

In the considered approximation (\( L\gg \xi \)) the critical current value is determined by the first term in the sum in Eq. (27):

where \( \theta(\infty) \) is determined by Eq. (6) with \( n=0 \), that is \( \omega=\pi T \). The expression (28) is an analog of the formula (2) derived in Ref.[16] for SNS structures with rigid boundary conditions at the SN boundaries. Unlike from Eq. (2), the expression (28) takes into account both the finite transparency of the SN boundaries and the delocalization of the weak-link region.

Note that the expression (27) is also valid in the limit of large \( \gamma_{BM} \gg 1 \), if the distance \( L \) between the SN electrode is not too small, so that the sum in Eq. (27) converges at

Theoretical results given above explain how \( T_{Th} \) can be determined on the basis of the available (calculated or experimentally obtained) \( I_c(T) \) dependence. Then using the formula (19) one can find such an important parameter for practical applications as the effective geometric size of the SN-N-NS Josephson contacts

Note that Eq. (30) is a direct consequence of Eq. (19) and is valid up to \( \gamma_{BM}\approx 100 \), as it can be observed from the comparison of the exact (16) and asymptotic (19) solutions for \( E_{T} \) in Figure 2. 

Our experimental study of a supercurrent transport across Nb/Cu-Cu-Cu/Nb34 and Nb/Au-Au-Au/Nb[39, 41] bridges has shown that the shape of the exponentially-decreasing dependences of \( I_c(T) \) in a wide temperature range closely resembles that shown in Figure 3. At \( \gamma_{BM}\lesssim 5 \) and large values of \( L\gtrsim 4\xi_N \) there is the transition at \( T\approx T_c (\xi_N /L)^2 \) from a sharp rise of \( I_c(T) \) to a smoother saturation at \( T\ll T_c \) as temperature decreases. At \( \gamma_{BM} \gtrsim 5 \) and small values of \( L\lesssim 4 \xi_N \) the change in the slope of the \( I_c(T) \) dependence takes place at \( T\approx T_c / \gamma_{BM} \).

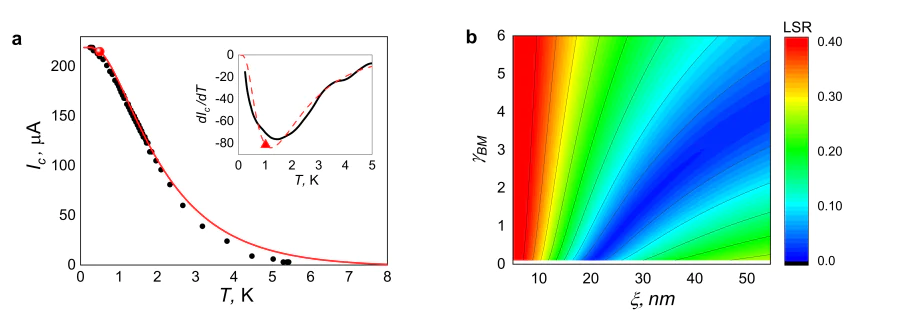
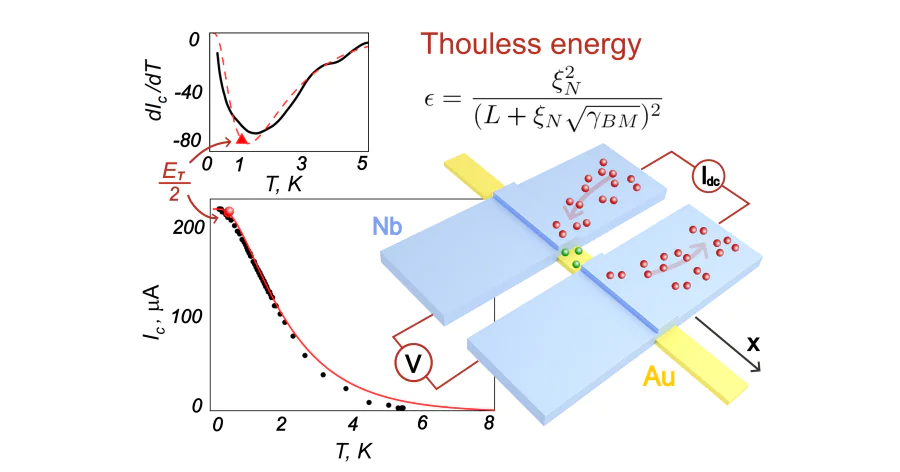
In Figure 4a we show the most recent experimental data for the Nb/Au-Au-Au/Nb Josephson bridge with a diffusive Au stripe operating as weak link. This structure was fabricated by magnetron sputtering and lift-off lithography. Further information concerning the fabrication process can be found in Refs.[39, 41, 51]. The approximate distance between the SN electrodes can be estimated as \( L\approx 160\, \textrm{nm} \) based on the scanning electron microscopy (see Figure 1b). The thicknesses of niobium and gold layers are equal approximately \( 70\, \textrm{nm} \) and \( 32\, \textrm{nm} \), respectively.

To compare the experimental data presented in Figure 4a with the results of the theoretical calculations, we construct a map which shows the dependence of the standard deviation between the experimental data and calculated dependence. The least-squares calculation of the standard deviation of the theoretical values of the critical current from the experimentally obtained points is shown in Figure 4b. This procedure results in a detection of a valley on the \( \gamma_{BM}-\xi \) diagram where the experimental points agree quite well with the theoretical calculation. It can be seen that the presence of two free parameters \( \gamma_{BM} \) and \( \xi \) does not lead to unique fitted solution. For different sets of \( \gamma_{BM} \) and \( \xi \) the formula (19) gives different \( E_{T} \) values.

Figure 4

a – Temperature dependence of the critical current \( I_c(T) \) for the NbAu-Au-AuNb bridge with the length of the weak link \( L=160\, \textrm{nm} \) (black circles) and numerical fits in the framework of the model (20)-(25) calculated at \( \xi_N=23\, \textrm{nm} \) and \( \gamma_{BM}=0.12 \) (red line). The red dot marks the temperatures corresponding to the halfed Thouless energy \( E_T/2 \). The inset shows the derivative \( dI_c(T)/dT \) of the interpolated experimental (black solid line) and model (red dashed line) \( I_c(T) \) dependencies. b – The least-squares residual between the experimental data and the model fits in the \( \gamma_{BM}-\xi \) plane of the parameters.

It should be noted that for the considered case the expression (19) allows us to specify the range of parameters in which it is worthwhile to search for a solution of the system at sufficiently large effective bridge lengths \( L \gtrsim 5 \xi \) and transparent interfaces \( \gamma_{BM} \lesssim 1 \). As an example, in Figure 4a we have shown one of possible approximation of the experimental dependence Ic(T) with the solution of the Usadel equations obtained for \( \xi_N=23\, \textrm{nm}  \) (\( L/\xi_N \approx 7 \)) and \( \gamma_{BM}=0.12 \) (red line). A large red dot on this graph marks the temperature \( T\approx 0.5\, \textrm{K} \), which corresponds to \( E_T/2 \) [see Eq. (19)]. The inset in Figure 4a shows the derivative of the theoretical \( dI_c/dT \) dependence (red dashed line) and the interpolation curve obtained for the experimental points. The red triangle 50 also marks the point where the temperature \( T\approx 1\, \textrm{K} \) coincides with the value corresponding to \( E_T \). It is located near the minimum of the derivative \( dI_c/dT \).

It should be emphasized that according to Eq. (30) for \( L/\xi_N \approx 7 \) and \( \gamma_{BM}=0.12 \) the effective size of the structure \( L_{\rm eff}\approx 7.3 \xi_N \) is actually determined by the distance between the electrodes \( L \). In this case, the features of the shape of the dependence \( I_c(T) \) are due to the transition from exponential to power laws of growth of Ic with decreasing temperature. As it can be illustrated in Figure 3, the position of these features correlates quite well with \( T_{Th} \). For shorter bridges (\( L\lesssim 3\xi \)) the \( I_c(T) \) dependences are smoother and the bending of the curves \( dI_c(T)/dT \) at \( T=E_{T}/2 \) are not as clear as for large \( L \) values. Also, in these case the interface parameter \( \gamma_{BM} \) increases resulting in a change of the shape of the \( I_c(T) \) dependence.

Thus, we have shown that the expression (19) can be used to determine the range of parameters in which the optimal approximation of the experimental results should be sought. For a more unambiguous extraction of the structural parameters from the experimental dependence \( I_c(T) \), it is necessary to approximate several samples simultaneously with different lengths between the electrodes \( L \), as done in Refs.[34, 41] and use additional data \( \rho_n \) and \( \gamma_B \) extracted from the temperature dependence of the normal-state resistance at \( T>T_c \). This approach allows one to significantly reduce the range of parameters for the best fitting by the microscopic model. However, it requires a complete construction of the parameter map, which is a rather time-consuming.

We demonstrate that the theoretical curve fits the experimental data well at \( T\lesssim 4\, \textrm{K} \). The observed discrepancy between the theoretical predictions and the experimental data at higher temperatures (\( T \gtrsim 4\, \textrm{K} \)) may be due to the following reasons.

Possible difference in the critical temperature of the region of the S layer adjacent to the N-film \( T_{cl} \) compared to the measured \( T_c \) of the bulk S electrode, as well as coordinate dependence of \( T_{cl} \). Another factor could be an inhomogeneity of the transparency of the NS boundaries, caused both by mechanical stresses at the NS interfaces, and their roughness. All these factors lead to the appearance of inhomogeneous island-type superconductivity in the N-layer which is more pronounced at \( T\to T_c \), i.e., to the appearance of the dependence \( \delta(x) \) in Eq. (22), which was not considered in the developed theory.

It should be noted that such a successful coincidence of the Thouless energy values found from the numerically calculated dependences \( I_c(T) \) and ones based on expression (19) does not mean that the \( E_{T} \) values determined from the shape of the experimental curves \( I_c(T) \) will lead to the same \( L_{\rm eff} \) value determined by Eq. (30). A deviation of the experimentally determined \( L_{\rm eff} \) value and the effective length defined by Eq. (30) may be due to the fact that some constrains controlling the applicability of the considered one-dimensional SN-N-NS contact are not realized experimentally.

Such restrictions include:

1. The smallness of the N-layer thickness compared to the decay length \( \xi_N \) . When using low-resistivity normal metals (Al, Au, Ag), the closeness of \( d \) to \( \xi_N \) can lead partial suppression of superconductivity in the S-layer near the SN boundary[52, 53].

where \( \rho_S \) and \( \xi_S \) are normal-state resistivity and coherence length of the S-film. Going beyond the one-dimensional approximation, the temperature \( T_{Th} \) actually decreases as d increases[54]. This automatically leads to an increase in the effective size of the SN-N-NS structure with respect to the \( L_{\rm eff} \) value defined by expression (30).

2. The boundary condition (25) states that the current flowing through the N-layer of the SN composite electrode is negligible compared to the current that has entered the S-layer of the electrode, i.e.

where \( d_S \) is the thickness of the S-film. A violation of this constraint should lead to the appearance of the dependence of the phase difference \( \varphi \) on the \( x \)-coordinate (see also the discussion in point 4 below).

3. At any point of the SN boundary, the density of the supercurrent injected from the normal metal through this interface into the S-layer should be less than the critical current density controlled by the finite transparency of this boundary, i. e.

4. The final constrain arises from the assumption that the phase difference \( \varphi \) appearing in Eqs. (20) and (22) is independent of the \( x \)-coordinate. This assumption is valid for \( x\gg L/2 \). Away from the N-NS boundary, the superconducting current is uniformly distributed across the thickness of the NS electrode. The current flows along the \( 0x \) direction, so the current lines do not cross the NS boundary. As a result, at \( x\gg L/2 \) the phase of the order parameter in each cross sections of the NS electrode turns out to be equal to the phase of the anomalous Green’s functions in both N and S-layers, and the \( \varphi(x) \) function turns out to be a value independent of \( x \) (see Ref.[11] for details).

Thus, through analytical evaluations and numerical calculations, we have shown that the Thouless energy in Josephson SN-N-NS bridges strongly depends on the resistance of the SN interface. The Thouless energy decreases by several times as this resistance increases compared to the SNS sandwich-type contact. We have also specified the range of validity of our analytical results, thus providing the possible explanations for the deviation of the experimentally obtained \( L_{\rm eff} \) from our analytical result (30).

The Thouless energy cannot be measured directly. Instead, the Thouless temperature can be determined by analyzing the shape characteristics of experimentally obtained \( I_c(T) \) dependences. Thouless temperature can be defined as the temperature corresponding to the saturation of the \( I_c(T) \) dependence at low temperatures and vanishing of the first derivative \( dI_c(T)/dT \). The use of this method for the experimental determination of \( T_{Th} \) requires measurements at rather low temperatures, which causes additional difficulties in finding \( T_{Th} \). We have shown that the transition from the study of the dependence \( I_c(T) \) to the determination of peculiar points on the temperature dependences of \( dI_c(T)/dT \) located at \( T \approx E_{T}/2 \) and \( T \approx E_{T} \) allows us to estimate the \( E_{T} \) value in the range of temperatures more convenient for measurements.

Our numerical calculations carried out in the framework of the one-dimensional SN-N-NS model of the Josephson SN-N-NS structure have shown that there is a relationship between the value of the Thouless energy \( E_T= 2 \pi T_{Th} \) determined in this way and the effective geometrical size of the structure \( L_{\rm eff} \) [see Eq. (30)] included in formula (19). The estimate of \( L_{\rm eff} \) obtained in this way is important in determining the limitations to miniaturization of the size of superconductor devices for processing analog and digital signals. It also provides additional information on the relationship between important technological parameters such as the NS electrode spacing \( L \), decay length \( \xi_N \) , and the parameter \( \gamma_{BM} \), which characterizes the transparency of NS boundaries.

We are grateful to A. I. Zaikin and A. A. Golubov for the discussion of the results obtained. A.N. thanks the support of the Foundation for the Development of Theoretical Physics and Mathematics ”BASIS”. The authors are grateful to MIPT Collective Use Center for providing facilities for samples fabrication. The experiments were carried out with the support of the Russian Science Foundation, Grant No. 23-72-30004 (https://rscf.ru/project/23-72-30004/).

Corresponding author: Sergey V. Bakurskiy, orcid.org/0000-0002-6010-6697, e-mail r3zz@mail.ru.

The authors declare no competing financial or non-financial interests.