Néel proximity effect in superconductor/antiferromagnet heterostructures

Superconducting proximity effect in mesoscopic heterostructures composed of conventional superconductors and normal, that is nonsuperconducting and nonmagnetic, metals (S/N heterostructures) is a penetration of Cooper pairs from a superconductor into an adjacent nonsuperconducting material with partial suppression of the superconducting order parameter in the superconductor near the interface. Conventional superconductors are formed by spin-singlet Cooper pairs[1, 2] and, therefore, they induce spin-singlet superconducting correlations in the adjacent normal metal. If a normal metal is replaced with a ferromagnet, the spin-singlet pairs, which penetrate into the ferromagnet, are partially converted into their spintriplet counterparts due to the presence of a macroscopic spin-splitting field in it[3-5]. Simultaneously the triplet pairs are also induced in the superconductor due to an inverse proximity effect. The same effect occurs if a thin superconducting film is subjected to a parallel magnetic field or if the superconductor is contacted with a ferromagnetic insulator[6]. The triplet pairs are produced at the expense of the singlet ones. This weakens the conventional superconducting state and lowers the critical temperature[7-9]. The generation of triplet Cooper pairs in superconductor/ferromagnet (S/F) heterostructures brought a lot of new exciting physics[3, 4] and gave a powerful impulse to development of superconducting spintronics[5, 10, 11].

Now what is about the proximity effect in superconductor/antiferromagnet (S/AF) heterostructures? Naively, since the net magnetization in an antiferromagnet averaged over the size of a typical Cooper pair vanishes, one should expect that S/AF heterostructures behave like S/N heterostructures from the point of view of the proximity effect. This means that (i) only singlet pairs can penetrate into the antiferromagnetic metal, and (ii) a superconductor interfaced to antiferromagnetic metal or insulator via a compensated interface is expected to experience no net spin-splitting and reduction in critical temperature[12]. Any macroscopic spin-splitting in S/AF heterostructures is only expected via an uncompensated (non-zero) interface magnetization. Indeed, it was predicted that the uncompensated interface induces a spinsplitting field in thin-film S/AF bilayers[13], which can result in some physical effects similar to thin-film S/F heterostructures[5], for example, in the giant thermoelectric effect[14], the anomalous phase shift[15] and anisotropy of the critical current in S/AF/S Josephson junctions with spin-orbit coupling[16].

However, it was realized long ago that in fact antiferromagnetism influences superconductivity not only via the uncompensated interface magnetization. In particular, it was reported that in antiferromagnetic superconductors the staggered exchange field suppresses superconductivity due to changes in the density of states and due to atomic oscillations of electronic wave functions[17]. The atomic oscillations of the electronic wave functions in antiferromagnetic materials also lead to the fact that nonmagnetic impurities in antiferromagnetic superconductors behave like effectively magnetic and additionally suppress superconductivity[17]. Further the theory taking into account the suppression of superconductivity by magnetic impurities was also developed for S/AF heterostructures[18, 19]. Several experiments have found that AFs lower the critical temperature of an S layer[20-23], despite there is no net spin-splitting. In some cases, the effect has been comparable or even larger than that induced by a ferromagnet layer[22]. Of course, a number of physical reasons can contribute to this observation. First, an AF doubles the spatial period of the lattice due to its antiparallel spins on the two sublattices. This can open a bandgap in the adjacent conductor, which may reduce the normal-state density of states in S, and thus suppress superconductivity[17, 24]. Second, partially the suppression can result from the uncompensated magnetization of the S/AF interface, which seems to be common in experiments[13, 25-27] and induces a spin-splitting and spin-flipping disorder in the superconductor, just like a ferromagnet[13]. Furthermore, the nonmagnetic disorder in the S/AF system also suppresses superconductivity, as it was mentioned above. Although all these physical effects are likely present in real systems, they are not associated with a physics of proximity-induced triplet superconducting correlations, which are a cornerstone of the physics and applications of S/F hybrids. Therefore, an important question arises whether triplet correlations in S/AF hybrid systems can arise only due to uncompensated surface magnetization or the Néel magnetism itself is also capable to generate new types of superconducting proximity effect.

Some unconventional for S/N heterostructures physical effects in S/AF hybrids with compensated interfaces were reported in the literature. For example, unconventional Andreev reflection and bound states at such S/AF interfaces have been predicted[28, 29]. The atomic-thickness \( 0-\pi \) transitions in S/AF/S Josephson junctions were investigated theoretically[30-32], an analysis of a hybrid comprising a ferromagnet and a compensated AF interfaced with an S suggested the interface to be spin-active[33]. All these results indicated that a key piece of understanding of the physics of S/AF hybrids was missing.

Further it was found that in spite of the absence of a net magnetization, the Néel magnetic order of the AF induces spin-triplet correlations at S/AF interfaces, which penetrate both into the superconductor and into the metallic antiferromagnet[34]. Their amplitude flips sign from one lattice site to the next similar to the Néel magnetic order in the AF. These correlations were called Néel triplet Cooper pairs. The goal of this review is to discuss the current understanding of the fundamental physics of these Néel triplet correlations and their physical manifestations.

Let us consider an antiferromagnetic insulator interfaced via a compensated interface to a thin conventional \( s \)-wave superconductor (Figure 1a). The system can be described by the following tight-binding Hamiltonian:

Figure 1

a – Sketch of the antiferromagnetic insulator with a compensated interface attached to the thin superconductor. b – Spatial variation of the amplitude \( F_{\boldsymbol{i}}^t \) of the triplet correlations. Each colored square codes the value of \( F_{\boldsymbol{i}}^t \) at a given site. An alternating sign of the correlations in S-layer commensurates with the Néel order in the AF-layer along the interface direction. The picture is adopted from Ref. [34].

where \( \boldsymbol{i}= (i_x,i_y)^T \) is the radius vector of the site and Greek letters correspond to the spin indices. \( \langle \boldsymbol{ij} \rangle \) means summation over the nearest neighbors. Here, \( \Delta_{\boldsymbol{i}} \) and \( \boldsymbol{h}_{\boldsymbol{i}} \) denote the on-site superconducting order parameter and the magnetic exchange field at site \( \boldsymbol{i} \), respectively; \( \hat c_{\boldsymbol{i} \sigma}^\dagger \) and \( \hat c_{\boldsymbol{i} \sigma}) \)) are operators of creation and annihilation an electron with spin \( \sigma = \uparrow,\downarrow \) on the site \( \boldsymbol{i} \); \( t \) denotes the nearest-neighbor hopping integral; \( \mu \) is the chemical potential; \( \hat n_{\boldsymbol{i} \sigma} = \hat c_{\boldsymbol{i} \sigma}^\dagger \hat c_{\boldsymbol{i} \sigma} \) is the particle number operator at the site \(\boldsymbol{i} \). We also define the vector of the Pauli matrices in spin space \( \boldsymbol{\sigma} = (\sigma_x, \sigma_y, \sigma_z)^T \). We assume that the antiferromagnet is of G-type, therefore the exchange field inside the antiferomagnet can be written in the form \( \boldsymbol{h}_{\boldsymbol{i}} = (-1)^{i_x+i_y} \boldsymbol{h} \). Axes \( x \) and \( y \) are taken normal to the S/AF interface and parallel to it, respectively. Hereafter we use the system of units, in which the reduced Planck constant \( \hbar \) and the Boltzmann constant \( k_B \) are equal to unity, for the sake of compactness.

The Hamiltonian (1) can be diagonalized by the Bogolubov transformation[34]. Further one can investigate the structure of the superconducting correlations at the S/AF interface using the solutions of the resulting Bogolubov-de Gennes equation. The anomalous Green’s function in the Matsubara representation can be calculated as \( F_{\boldsymbol{i}, \alpha \beta} = - \langle \hat c_{\boldsymbol{i} \alpha}(\tau) \hat c_{\boldsymbol{i} \beta}(0) \rangle \), where \( \tau \) is the imaginary time. The component of this anomalous Green’s function for a given Matsubara frequency \( \omega_m = \pi T(2m+1) \) is calculated as follows:

where \( u_{n,\alpha}^{\boldsymbol{i}} \) and \( v_{n,\alpha}^{\boldsymbol{i}} \) are electron and hole parts of the two-component eigenfunction of the Bogolubov-de Gennes equation, corresponding to the \( n \)-th eigenstate, \( \varepsilon_n \) is the eigenenergy of this state, and \( \alpha \), \( \beta \) are spin indices. Only off-diagonal in spin-space components, corresponding to opposite-spin pairs, are nonzero for the case under consideration. The singlet (triplet) correlations are described by \( F_{\boldsymbol{i}}^{s,t}(\omega_m) = F_{\boldsymbol{i},\uparrow \downarrow}(\omega_m) \mp F_{\boldsymbol{i},\downarrow \uparrow}(\omega_m) \). The on-site triplet correlations are odd in Matsubara frequency, as it should be according to the general fermionic symmetry. The spin-triplet correlations amplitude \( F_{\boldsymbol{i}}^t \) at each lattice site with the radius-vector \( \boldsymbol{i} \) is evaluated by summing the anomalous Green’s function over the positive Matsubara frequencies \( F_{\boldsymbol{i}}^t = \sum \limits_{\omega_m>0} F_{\boldsymbol{i}}^t(\omega_m) \).

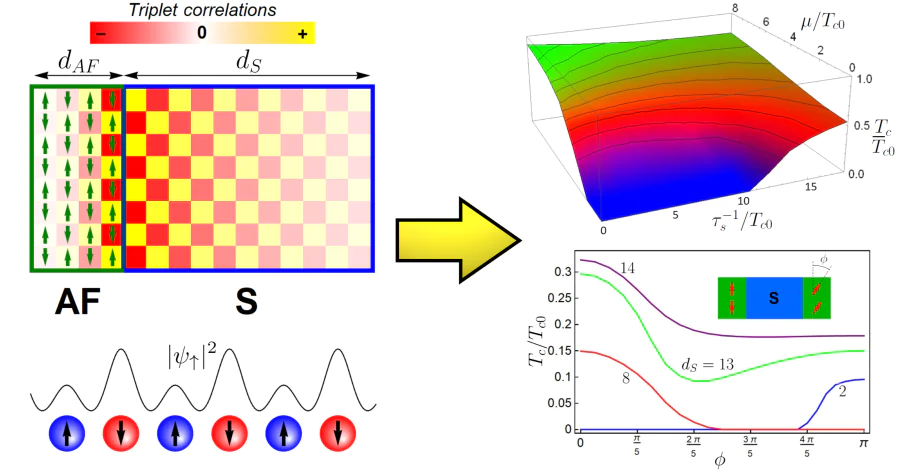
Figure 1b plots the spatially resolved spin-triplet pairing amplitude in the S/AF bilayer. A clear imprinting of the AF Néel ordering is seen on the triplet pairing amplitude in the direction parallel to the interface: an alternating sign of the correlations in the S layer is clearly visible. This perfect picture is disturbed in the direction perpendicular to the interface due to the absence of the translational invariance in this direction. We will get back to physical reasons of the disturbance in Section 4 of this review.

The physics related to the proximity-induced Néel triplet correlations can be also described in the framework of the two-sublattice quasiclassical theory in terms of the Eilenberger equation, which was developed in Ref. [34].

What is the physical origin of the Néel Cooper pairs? The essential physics is captured already within a one dimensional (1D) model[34] considering 1D AF covered by 1D superconductor. Therefore, the electron wavevector bears only one component which is along the interface.

In the absence of the antiferromagnet the normal-state electronic dispersion of S-metal can be depicted as in Figure 2 with a Brillouin zone (BZ) \( pa \in [-\pi,\pi] \), where a is the lattice constant. Within this single-sublattice dispersion the Néel magnetic order in AF causes scattering between electronic states that differ by the wavenumber \( Q_{1D} = \pi/a \) (so-called Umklapp scattering[35-37]) at the S/AF interface. Thus, the AF converts conventional spinsinglet pairing between electrons with momenta \( +p_0 \) and \( -p_0 \) at the Fermi surface (blue line in Figure 2) into the Néel spin-triplet pairing between, for example, \( +p_0 \) and \( -p_0 + Q_{1D} \) (green line in Figure 2). In real space such a pairing changes sign from a site to its nearest neighbor similar to the Néel order with the wavenumber \( Q_{1D} \). The antiferromagnetic gap opening has been disregarded in the present simplified figure.

Figure 2

Electron dispersion \( \xi_{\pm}(p) = \mp 2t \cos pa - \mu \) of the normal-state S in the reduced Brillouin zone (BZ) \( pa \in [-\pi/2,\pi/2] \) considering a 1D system with two sites in the unit cell (solid curves). The electron energy defined by \( \xi_{\pm}(p) \) is counted from the Fermi surface. The reciprocal lattice vector due to the periodicity enforced by the AF is \( Q_{1D} = \pi/a \). The spectrum branches are doubled in the BZ due to the reduction of the BZ volume. The spectrum of the original 1D superconductor with one site in the unit cell in the BZ \( pa \in [-\pi,\pi] \) is shown by dashed curves. The blue line indicates ordinary pairing between \( p_0 \) (state 1) and \( -p_0 \) (state 2) electrons corresponding to the zero total pair momentum. The green line indicates Néel pairing between \( p_0 \) (state 1) and \( - p_0+Q_{1D} \) (state 3) corresponding to the total pair momentum \( Q_{1D} \). The picture is adopted from Ref. [34].

Strictly speaking, to describe the whole S/AF system, we should use a unit cell with two sites in it, corresponding to two sublattices of the antiferromagnet with opposite magnetizations. Within this two-sublattice picture, we now have two bands in the electronic dispersion. What appeared as pairing between \( +p_0 \) and \( -p_0 + Q_{1D} \) states in the single-sublattice picture is actually pairing between the \( +p_0 \) state from one band with the \( -p_0 \) state from the other band, as depicted in Figure 2. Therefore, we conclude that the Néel pairing is the interband pairing.

Due to its interband origin the Néel triplet pairing is very sensitive to the value of the chemical potential in the material, where it is induced. It is in sharp contrast with the usual triplet pairing induced by the proximity effect at S/F interfaces, which is insensitive to the value of the chemical potential because of its intraband nature. To see the dependence of the Néel pairing on the chemical potential, let us have another look at Figure 2. Taking into account that \( p_0 \) is defined from the condition \( \xi_+(p) = -2 t \cos p_0 a - \mu = 0 \) one immediately obtains that \( \xi_1 - \xi_{3'} = 2\mu \). That is, the energy difference between states \( 1 \) and \( 3' \) grows with \( \mu \), thus reducing the efficiency of pairing. This qualitative picture was supported in Ref. [34] by strict calculations performed in the framework of the two-sublattice quasiclassical theory.

Figure 3 represents the results of calculation of the Néel triplet amplitude \( F^t_A \) in a thin superconductor proximitized by an AF insulator. Such a thin-film superconductor with the thickness \( d_S \ll \xi_S \), where \( \xi_S \) is the superconducting coherence length, can be considered as a homogeneous superconductor under the influence of an effective exchange field of the Néel type \( h_{\mathrm{eff}} \)[13, 34], which accounts for the influence of the AF insulator on the superconducting film. In Figure 3 the Néel triplet amplitude is plotted for different values of the chemical potential \( \mu \) of the superconductor and different amplitudes of the effective exchange field \( h_{\mathrm{eff}} \equiv |\boldsymbol{h}_{\mathrm{eff}}| \). It is clear that for a given value of \( h_{\mathrm{eff}} \) the Néel triplet amplitude indeed weakens upon increase in \( \mu \). The amplitude of conventional triplet correlations induced in the same thin-film superconductor by proximity to a ferromagnetic insulator producing the effective exchange field of the same amplitude \( h_{\mathrm{eff}} \) (homogeneous, not Néel) is also shown for comparison (see purple curve in Figure 3).

Figure 3

Anomalous Green’s function of the Néel triplet correlations as a function of \( h_{\mathrm{eff}} \) for different values of \( \mu \). Each line ends at the critical value of \( h_{\mathrm{eff}} \) corresponding to the full suppression of superconductivity. \( T_{c0} \) is the critical temperature of the superconductor without proximity to a magnet. The picture is adopted from Ref. [34].

The weakening of the Néel triplet correlations with increasing chemical potential does not mean that they are completely suppressed at high values of the chemical potential (\( \mu \gg T_{c0} \)), when the filling factor in the superconductor is far from half filling of the conduction band. Here \( T_{c0} \) is the critical temperature of the superconductor in the absence of the proximity to the AF. The amplitude of the Néel triplet correlations increases with increasing effective exchange field \( h_{\mathrm{eff}} \), as it is seen from Figure 3. It was shown in Ref. [38] that at \( (h_{\mathrm{eff}}, \mu) \gg T_{c0} \) the amplitude of the Néel triplet correlations is only determined by the ratio \( h_{\mathrm{eff}}/\mu \) and reaches its maximal value at the line \( h_{\mathrm{eff}}/\mu = {\rm const} \approx 0.8 \). This tendency is demonstrated in Figure 4 . For larger values of this parameter the superconductivity in the system is fully suppressed.

Figure 4

Amplitude of the triplet correlations relative to the singlet amplitude as function of \( h_{\mathrm{eff}} \) and \( \mu \) at \( T \to T_c \). Inset: region \( (h_{\mathrm{eff}},\mu) \sim T_{c0} \) on a larger scale. The picture is adopted from Ref. [34].

Now we demonstrate that the Néel triplet correlations suppress the superconductivity at S/AF interfaces and, in particular, they suppress the superconducting critical temperature of thin-film superconductors proximitized by antiferromagnetic insulators. The effect is analogous to the well-known suppression of superconductivity by proximity-induced triplets at S/F interfaces[4]. Again we discuss a thin-film superconductor with \( d_S \ll \xi_S \) in proximity to an antiferromagnetic insulator.

The dependence of the critical temperature of the S/AF bilayer on the effective exchange field is presented in Figure 5 for different values of the chemical potential. The critical temperature is indeed suppressed by the staggered exchange field \( h_{\mathrm{eff}} \). The efficiency of suppression by the staggered field is of the same order, and even higher, as the suppression by the ferromagnet with the same absolute value of the exchange field. The stronger suppression of the superconductivity by the staggered exchange as compared to the uniform ferromagnetic exchange field is explained by the presence of the antiferromagnetic gap at the Fermi surface, which prevents electronic states inside this gap from superconducting pairing. The superconductivity suppression for a given \( h_{\mathrm{eff}} \) becomes weaker for larger values of the chemical potential, what is explained by weakening of the Néel triplet correlations upon increase of \( \mu \).

Figure 5

Critical temperature of the S/AF bilayer as a function of \( h_{\mathrm{eff}} \) for different values of \( \mu \). Black line represents the dependence \( T_c(h_{\mathrm{eff}}) \) for an S/F interface with a ferromagnetic insulator producing the same value of the effective exchange field (but homogeneous, not staggered) in the superconductor. The picture is partially overlapped with an analogous picture from Ref. [34].

Following to Ref. [39] we would like to discuss, what happens with the proximity effect in heterostructures composed of superconductors and canted antiferromagnets. We consider a bilayer structure consisting of an insulating AF with canted sublattice magnetizations exchange coupled to an adjacent S. The sketch of the system is shown in Figure 6. The canting angle is \( \theta_t \). For \( \theta_t=0 \) the considered AF becomes a collinear antiferromagnet with the axis of magnetic moments along the \( x \)-direction. As we increase the value of \( \theta_t \), the canted-AF acquires a net magnetization along the \( y \)-direction. So the canted-AF can be decomposed into an antiferromagnetic component (along the \( x \)-axis) and a ferromagnetic component (along the \( y \)-axis).

Figure 6

Sketch of the system and key physics of the proximity effect at S/canted AF interfaces. Equal-spin and zero-spin triplet correlations are generated in a conventional \( s \)-wave spinsinglet superconductor when it is interfaced with a canted antiferromagnet (canted-AF). The equal-spin triplet correlations result from the intrinsic noncollinearity between the two AF sublattice magnetizations. The canting angle \( \theta_t \) allows one to vary the magnet from being a collinear AF (\( \theta_t = 0 \)) to a ferromagnet (\( \theta_t = \pi/2 \)). The picture is redrawn after Ref. [39].

Chourasia et al.[39] investigated the spin-triplet correlations and calculated the critical temperature of the S as functions of the canting angle in the AF, which allows us to continuously tune the AF from its collinear antiparallel state to that effectively becoming in F. In general, the vector amplitude of the triplet superconducting correlations induced in the S-layer by proximity to the AF can be written as \( {\bf F}^t_j=F^{t,x}_j {\bf e}_x + F^{t,y}_j  {\bf e}_y + F^{t,z}_j {\bf e}_z \). It always has a component aligning with the local exchange field whether the magnetization of a magnet (either ferromagnet or antiferromagnet) is homogeneous or inhomogeneous. If the magnetization is inhomogeneous, other components, not coinciding with the direction of the local exchange field, appear[3]. In the considered case the magnetization is obviously inhomogeneous due to canting. For this reason all three components of the triplet vector are nonzero.

The dependence of these spin-triplets on the canting angle is presented in Figure 7. At \( \theta_t = 0 \) only \( F^{t,x} \) component is nonzero. It corresponds to the pure Néel triplet order discussed above. The Néel structure of this component was demonstrated explicitly[39]. This component decreases as \( \theta_t \) goes from 0 to \( \pi/2 \) (Figure 7b) and vanishes at \( \theta_t = \pi/2 \) because the Néel triplets are absent in the purely ferromagnetic state. It is also seen that the amplitude of this component decreases as \( \mu \) increases in agreement with the general dependence of the Néel triplets on the chemical potential, discussed above. Here the chemical potential is determined via the filling factor \( f \), which is the fraction of filled electronic states in the system: \( f=0.5 \) (half-filled band) corresponds to \( \mu=0 \).

Figure 7

a, b, c – Variations of the triplet correlations with the canting angle \( \theta_t \) for different filling factors \( f=0.5 \) (\( \mu=0 \)) and \( f=0.6 \) \( (\mu/T_{c0} \approx 65) \). These panels show the average magnitudes of the normalized spin-triplet correlation \( F^{t,z} \) (panel a), \( F^{t,x} \) (panel b), and \( F^{t,y} \) (panel c). The averages are taken over all superconducting sites and they are denoted via an overhead bar. The picture is adopted from Ref. [39].

The component \( F^{t,y} \) increases with the canting angle and it appears to be caused primarily by the net magnetization (Figure 7c). It was directly checked that it is a conventional triplet component without the Néel structure. It is maximal in the purely ferromagnetic state. \( F^{t,z} \) is also found to be of the Néel type (Figure 7a). It appears due to the noncollinearity of two sublattices. Its Néel character can be understood in terms of this noncollinearity. Hopping from one lattice site to the next, the angle between the spin-splitting at the site and its direct neighbors changes its sign. It is interesting that it vanishes at \( \mu=0 \) (\( f=0.5 \)) for all canting angles. The physical reason is that for \( \mu \approx 0 \) the antiferromagnetic gap opens in the superconductor in the vicinity of the normal state Fermi surface. In this case the most important contribution to the pairing correlations is given by the electronic states at the edge of the gap. They correspond to \( \xi_\pm \approx 0 \), what means that the electrons are practically fully localized at one of the sublattices. Consequently, they only feel the magnetization of the corresponding sublattice, which is homogeneous. As a result, the noncollinearity does not affect the \( z \)-component or the triplet correlations. However, for non-zero \( \mu \) (away from the half-filling case) \( F^{t,z} \) increases from zero to a finite value as we go from a collinear antiferromagnetic alignment to the maximal noncollinearity between the sublattice magnetic moments, and then it decreases back to zero for the ferromagnetic alignment (Figure 7a).

As it was already discussed, the critical temperature of superconductor/magnet heterostructures is suppressed by triplet correlations, both of conventional type and the Néel type. Therefore, it is natural to expect that the critical temperature of the S/AF bilayers with canted antiferromagnets is always suppressed with respect to the critical temperature of the isolated superconductor \( T_{c0} \). It was found[39] that it is indeed the case. However, the physics of the suppression is very interesting. In the framework of our review here we encounter the first manifestation of the crucial dependence of the Néel triplets on the chemical potential and its physical consequence. It was obtained that the dependence of the critical temperature on the canting angle \( \theta_t \) is opposite near half-filling and far from half-filling. It is demonstrated by Figure 8 composed for \( f = 0.5 \) and \( \mu=0 \) (panel a), and for \( f = 0.6 \) and \( \mu \approx 65 T_{c0} \) (panel b). It is found that for \( \mu=0 \) the \( T_c \) value increases with \( \theta_t \) while it manifests the opposite dependence for \( \mu \neq 0 \).

Figure 8

a, b – Normalized critical temperature \( T_c \) vs. canting angle \( \theta_t \) for the filling factors \( f=0.5 \) (panel a) and \( f=0.6 \) (panel b) considering different values of the antiferromagnetic exchange field \( h \). \( \Delta_0 \) is the zero-temperature superconducting order parameter of the same superconductor without the AF-layer. The picture is adopted from Ref. [39].

For the case \( \mu = 0 \) presented in Figure 8a, a strong generation of the Néel triplets due to the interband pairing leads to the maximal Tc suppression at \( \theta_t = 0 \). Since the \( T_c \) suppression is stronger for the pure AF case (\( \theta_t = 0 \)) than for the pure F case (\( \theta_t = \pi/2 \)), the \( T_c \) value increases with \( \theta_t \). For the case of \( f = 0.6 \) (\( \mu \gg T_{c0} \)) and \( h \sim T_{c0} \) (\( h \equiv |\boldsymbol{h}| \)), the Néel triplets generation by the antiferromagnetic order is much weaker. On the other hand, the ordinary spin-triplets generation by a ferromagnet remain of the same order of magnitude as for \( f = 0.5 \). Thus, Tc is the largest for \( \theta_t = 0 \) and it decreases with \( \theta_t \).

In this section we discuss how the superconductivity in S/AF heterostructures is influenced by conventional nonmagnetic impurities and what is the role of the Néel triplets in this physics. Here we will have the second example of the crucial influence of the chemical potential on the physics of S/AF heterostructures.

First of all, we discuss how the Néel triplets behave in the presence of impurities. It was shown [34] that near half-filling state nonmagnetic disorder destroys the Néel spin-triplet correlations. The physical reason of the suppression of the Néel triplets by the nonmagnetic disorder is their interband nature. At the same time, at \( \mu \gg T_{c0} \) the interband Néel triplet pairing is suppressed. However, the Néel triplet correlations can be essential even at large values of \( \mu \), as it was demonstrated in Refs. [38, 39] and was discussed above in this review. In this case all pairing correlations are completely intraband, as it is shown in Figure 9a. It should be noted that the normal state eigenvectors of the electronic band crossed by the Fermi level represent a mixture of sign-preserving and sign-flipping components between the \( A \) and \( B \) sites of the same unit cell:

where

are the sign-preserving (flipping) amplitudes of the eigenvectors. Due to the presence of the sign-flipping component of the eigenvectors and its spin sensitivity, the singlet homogeneous pairing between \( \boldsymbol{p} \) and \( -\boldsymbol{p} \) states at the Fermi level (see Figure 9a) is inevitably accompanied by the Néel sign-flipping triplet component. As it can be seen from Eq. (4) the amplitude of the sign-flipping mixture is controlled by the ratio \( h_{\mathrm{eff}}/\mu \) and it is suppressed as μ increases, what is in agreement with the dependence of the Néel triplets on the chemical potential, presented in Section 2.3.

Figure 9

a, b – Electron dispersion of the normal-state in the reduced Brillouin zone (BZ) \( pa \in [-\pi/2, \pi/2] \). For simplicity of visualization a 1D system dispersion \( \varepsilon_N^{1D} = \mp \sqrt{\xi^2(p)+h_{\mathrm{eff}}^2} - \mu \) is demonstrated instead of a real dispersion \( \varepsilon_N^{3D} \). Here we take into account the opening of the antiferromagnetic gap due to \( h_{\mathrm{eff}} \). a – Case of large \( \mu \). The electronic states in the vicinity of the Fermi surface \( \varepsilon_N^{1D} = 0 \) allowed for pairing (pink region) do not involve the second electronic branch. Only \( (\boldsymbol{p}, -\boldsymbol{p}) \) intraband singlet and intraband Néel triplet pairs are present (dashed blue-green). b – Case of small \( \mu \) for comparison. Electronic states belonging to the both branches are present in the vicinity of the Fermi surface and are allowed for pairing. Both intraband singlet (blue) and interband Néel triplet pairs (green) exist. The picture is adopted from Ref. [38].

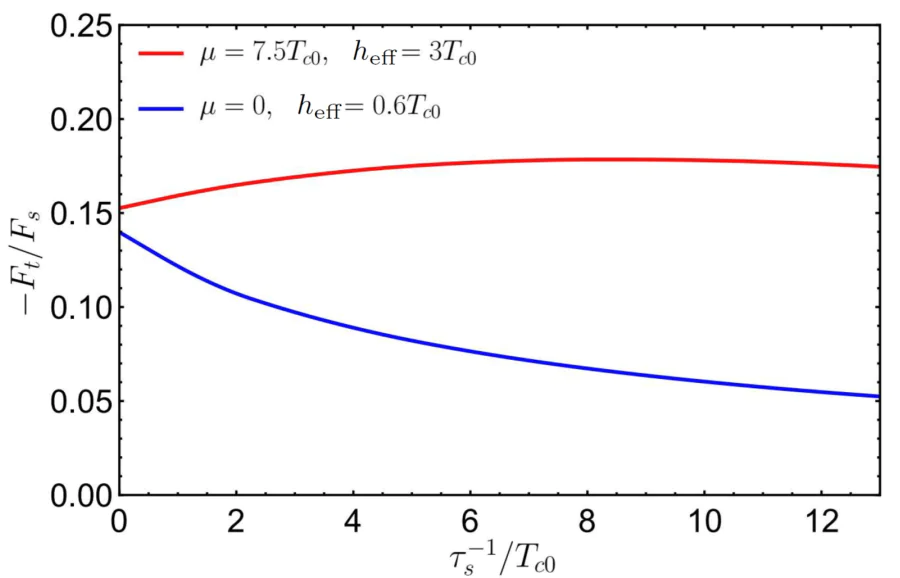
It is natural to expect that the \( s \)-wave intraband triplets are not sensitive to the influence of nonmagnetic impurities. Our calculations, performed in the framework of the non-quasiclassical Green’s functions approach, originally presented in Ref. [38] confirm these expectations. The dependencies of the Néel triplet amplitudes on the nonmagnetic impurity inverse scattering time \( \tau_s^{-1} \) s are demonstrated in Figure 10. It is seen that at \( \mu=0 \) the amplitude of the Néel triplet correlations is suppressed by impurities, as it was found in Ref. [34]. At rather large parameter \( \mu=7.5 T_{c0} \) we clearly see no suppression. Instead, a weak increase of the Néel triplet amplitude is observed. We cannot definitely say what is the reason for this weak increase. Probably it is related to the influence of impurities on the normal-state density of states (DOS).

Figure 10

Amplitude of the triplet correlations relative to the singlet amplitude as a function of the inverse impurity scattering time for a superconductor in the presence of the Néel-type effective exchange field \( h_{\mathrm{eff}} \). Different curves correspond to different values of the chemical potential \( \mu \).

What happens with the critical temperature of thin-film S/AF bilayers in the presence of impurities? Based on the results discussed in the previous subsection one can conclude that Tc should be enhanced with impurity scattering strength at small chemical potentials because of weakening the triplets, which are generated at the expense of singlets. It is indeed the case, as it is shown in the next subsection. But what we can expect at large \( \mu \)? Is the critical temperature only negligibly sensitive to impurities? The answer is that at large chemical potentials the critical temperature is suppressed by nonmagnetic impurities quite strongly. The mechanism of the suppression is not related to the Néel triplets. The amplitude of the wave functions of electrons is different for \( A \) and \( B \) sublattices [see Eq. (3)]. Physically it is because of the fact that for an electron with spin up it is energetically favorable to be localized on the \( B \) sublattice and for an electron with spin down — on the \( A \) sublattice. Thus, this sublattice-spin coupling in the presence of the Néel-type exchange field gives an effective magnetic component to the non-magnetic impurities. And it is well-known that magnetic impurities do suppress superconductivity[5]. This mechanism of superconductivity suppression by nonmagnetic impurities was originally discussed for antiferromagnetic superconductors[17]. Then it was realized that it also works for S/AF heterostructures[18, 19], where an appropriate quasiclassical theoretical formalism taking into account the destroying action of nonmagnetic impurities was developed[18] and the suppression of the critical temperature of S/AF bilayers with metallic antiferromagnets due to the nonmagnetic impurities was found[20].

The influence of nonmagnetic impurities on the critical temperature of thin-film S/AF bilayers, which can be effectively modelled as superconductors in a homogeneous effective Néel exchange field \( h_{\mathrm{eff}} \), in the full range of parameters of the bilayer was considered in Ref. [38].

We start with the discussion of two limiting cases. Figure 11 and Figure 12 demonstrate the critical temperature of the S/AF bilayer as a function of the inverse impurity scattering time \( \tau_s^{-1} \). The results shown in Figure 11 are calculated at \( \mu=0 \) and represent a typical example of the dependence in the regime when the interband Néel triplets are strong and play the role of the main depairing mechanism, and the impurities do not really work as effectively magnetic. It can be seen that at \( h_{\mathrm{eff}} \neq 0 \) the critical temperature grows with the disorder strength or even appears at some nonzero \( \tau_s^{-1} \). This behavior is explained by the presence of the Néel triplets, which suppress the critical temperature of the singlet superconductivity. In the clean limit \( \tau_s^{-1}=0 \) their amplitude is the maximal. Due to the interband nature of the Néel pairing they are gradually reduced with impurity strength and, consequently, the critical temperature grows.

Figure 11

Dependence of \( T_c \) on \( \tau_s^{-1} \) at \( \mu=0 \) for different effective exchange fields \( h_{\mathrm{eff}} \). \( T_c \) is normalized to the value of the critical temperature \( T_{c0} \) of the isolated S-film. The picture is adopted from Ref. [38].

Figure 12 corresponds to \( \mu= 150\,T_{c0} \). It represents the opposite limit when the interband Néel triplets are suppressed. Intraband Néel triplets are still there and they suppress superconductivity of the bilayer with respect to the case of an isolated superconductor, especially at large values of \( h_{\mathrm{eff}} \), as it is seen at \( \tau_s^{-1} = 0 \). However, the intraband Néel triplets are not sensitive to nonmagnetic impurities. The dependence \( T_c(\tau_s^{-1}) \) is dominated by the impurity suppression.

Figure 12

Dependence of \( T_c \) on \( \tau_s^{-1} \) at \( \mu=150\,T_{c0} \) for different effective exchange fields \( h_{\mathrm{eff}} \). The picture is adopted from Ref. [38].

Now, after considering the limiting cases we discuss the effect of nonmagnetic impurities on the superconductivity of the S/AF hybrids in the entire range of parameters. Figure 13 represents the behavior of the critical temperature in the \( \tau^{-1}_s-\mu \) plane for a given \( h_{\mathrm{eff}}=2.25 T_{c0} \). Front and back sides of the image correspond to the considered opposite limits. The front side is the limit of small μ, where Néel triplets dominate and, consequently, superconductivity is restored with increase in impurity strength. The back side corresponding to large μ, represents the suppression of superconductivity by nonmagnetic impurities. For intermediate \( \mu \) values there is a crossover between them. In particular, for a certain range of \( \mu \) a nonmonotonic dependence \( T_c(\tau^{-1}_s) \) is observed. The initial suppression of \( T_c \) is changed by some growth. This is because the singlet superconductivity is suppressed by the impurities more rapidly than the Néel triplets. This behavior is in sharp contrast with the behavior of a F/S bilayer, where the critical temperature is not sensitive to the nonmagnetic impurity concentration, and the magnetic impurities suppress the superconductivity[40]. Moreover, the properties of S/F bilayers is mainly not sensitive to the deviation from half-filling of the electronic spectrum unlike from S/AF hybrids.

Figure 13

Dependence of the critical temperature \( T_c \) on \( \tau_s^{-1} \) and \( \mu \) at \( h_{\mathrm{eff}}=2.25 T_{c0} \). The picture is adopted from Ref. [38].

It is worth noting that all the results discussed above are valid for the case of relatively weak disorder, which can be considered in the Born approximation. The issue about the influence of the strong disorder on superconductivity in S/AF heterostructures is yet to be explored. For the case of conventional \( s \)-wave superconductors it is known that a strong disorder can lead to a metal–insulator transition in the normal state, to the appearance of a pseudogap in spectrum and larger spatial fluctuations of superconductive pairing, what results in increased \( \Delta/T_c \) ratio[41-45]. Furthermore, Anderson localization and phase fluctuations, are more pronounced in low-dimensional structures, leading to the suppression of superconductivity. At the same time, the disorder can also result in a remarkable enhancement of superconductivity[46-52]. The stronger disorder increases spatial inhomogeneity, which enhances the local pairing correlations and superconducting gap, comparing with the clean system. Disorder-related effects are assumed to be responsible for a large increase of the critical temperature in the recently discovered superconducting NbSe₂ monolayers. Theoretical analysis attributes the enhancement to the disorder-induced multi-fractal structure of the electronic wave functions. Which of the listed possibilities are relevant to S/AF heterostructures is to be studied. This prospect for future work is especially interesting in view of the opposite effects of the weak disorder on superconductivity near half-filling and away from half-filling, what can make the physical picture of the effect of the strong disorder even richer.

Triplet pairs, originated from the singlet-triplet conversion in homogeneous superconductors under the action of a Zeeman field, are usually zero-momentum pairs[9], what means that their wave functions are uniform in real space. However, in some narrow regions of parameters an inhomogeneous superconducting state produced by singlet and triplet pairs with finite momentum of the pair, the so-called Fulde-Ferrel-Larkin-Ovchinnikov (FFLO) state, was predicted[53, 54]. One of the important properties of the triplet pairs generated at F/S interfaces, where the translational invariance is lost, is that the zero-momentum pairs, entering the ferromagnetic region from the superconductor, inevitably acquire a finite momentum of the pair[55, 56] due to the fact that the spin-up and spin-down electrons forming a pair have opposite potential energies in the macroscopic exchange field of the ferromagnet. Thus, the electrons residing at the same energy (at the Fermi surface) have not strictly opposite momenta in the ferromagnet (the absolute values of their momenta are different) and the pair as a whole has nonzero total momentum. The finite momentum is acquired both by singlet and triplet pairs, what allows us to refer to such state as a mesoscopic analogue of the FFLO superconducting state[53, 54]. The finite momentum, which the Cooper pair acquires in the exchange field of the ferromagnet, makes the pairing wave function oscillating. The resulting phase change across the ferromagnetic layer is responsible for the \( \pi \)-junction effects[4, 55, 57-61], which are widely used now in the superconducting electronics[62-64]. The interference of the incident and reflected oscillating wave functions determines the oscillatory phenomena of the critical temperature \( T_c \) versus the F-layer thickness in bilayers and multilayers, which have been widely studied both theoretically[65-70] and experimentally[71-75].

Naively, one does not expect that a Cooper pair penetrating into the antiferromagnet from the superconductor possesses a finite total momentum because (i) the average value of the exchange field in the antiferromagnet is zero, (ii) the quasiparticles spectrum is spin-degenerate and, therefore, (iii) spin-up and spin-down electrons, forming the pair, should have opposite momenta with equal absolute values \( \boldsymbol{p}_\uparrow = -\boldsymbol{p}_\downarrow \). In its turn, that means zero total momentum of the pair and, as a result, absence of the oscillations of the pair amplitude. However, it was shown that in the absence of the translational invariance in S/AF heterostructures (i. e., at S/AF interfaces or single impurities) the finite-momentum Néel triplet pairing occurs[76, 77]. It was demonstrated theoretically that the finite-momentum Néel triplet correlations at S/AF interfaces result in the oscillating dependence of the critical temperature on the thickness of AF-film[76]. There are a number of experimental works, where the critical temperature of S/AF bilayers with metallic antiferromagnets has been measured as a function of the AF thickness and the oscillating behavior was observed[20-22]. At the same time, in the regime, when the Néel triplets can be disregarded, this dependence has been calculated and no oscillations were reported[19]. Thus, oscillations of the critical temperature of S/AF bilayers can be viewed as a signature of the presence of finite-momentum Néel-type triplet correlations in the hetero-structure. In two following subsections we consider the physical nature of the finite-momentum Néel triplet pairing and discuss how it manifests in the critical temperature of S/AF bilayers with metallic antiferromagnets.

In Section 2.2 we discussed the qualitative mechanism of the Néel triplet pairing. It was shown that the Néel pairing is pairing of electrons having the momenta \( \boldsymbol{p} \) and \( -\boldsymbol{p} + \boldsymbol{Q} \), where \(  \boldsymbol{Q} \) is the reciprocal lattice vector due to the periodicity enforced by the AF ordering. In the 2D case it is \( \boldsymbol{Q} = (\pi/a,\pi/a) \). In real space this pairing manifests itself as the atomic-scale oscillations of the pair amplitude: it flips its sign from one site to its nearest neighbor. But if we only monitor on-site Néel triplet pairs for one of the sublattices, we see that the amplitude is homogeneous. Now let us consider a situation with broken translational invariance in the system. The simplest case is a plane S/AF interface. Previously we discussed mainly effectively homogeneous systems such as thin-film superconductors proximitized by AF insulators, which can be considered as homogeneous superconductors under the action of the Néel effective exchange field \( h_{\mathrm{eff}} \). The spatial dependence of the proximity effect in the direction perpendicular to the interface was neglected due to the small thickness of the S-film in the transverse direction. The only exception is Figure 1 of this review, where this simplification was not used. It is clear that the perfect Néel structure, which we see along the interface, is violated in the direction perpendicular to the interface. Even if we monitor the on-site Néel pairing at one of the sublattices, the corresponding amplitude has some oscillations. It is a signature of the formation of finite-momentum Néel triplet pairs due to scattering events at the interface. Now let us explain the mechanism of such pairing in more details.

If we consider a plane interface, which breaks the translational invariance along the \( x \)-direction, then it is convenient to choose the Brillouin zone (BZ) as shown in Figure 14. Due to the doubling of the unit cell BZ is compressed twice in the lateral direction along the \( y \)-axis. As a result, additional branches of the Fermi surface appear in the reduced BZ. Please note that such additional branches of the Fermi surface do not occur in the 1D case, considered in Section 2.2. Let us consider an electron \( (p_{x1}, p_y) \) incoming to the S/AF interface from the AF side (marked by 1 in Figure 14). Because of Umklapp scattering at the the S/AF interface this electron can be reflected as electron 3 from another branch, corresponding to the momentum \( (p_{x3}, p_y) \) (for the plane interface the component of the electron momentum \( p_y \) along the interface is conserved). That is why the electron 2 with momentum \( (-p_{x1}, p_y) \) can form not only a singlet zeromomentum Cooper pair with the electron 1, but also a Néel-type triplet pair with the electron 3, which has a finite total momentum \( \delta p = |p_{x3}-p_{x1}| \). The normal-state electron dispersion in the reduced BZ takes the form

Figure 14

Brillouin zone and Fermi surface (black curves) of the AF layer. Zero-momentum Cooper pair between electrons 1 and 2 is schematically shown by black arrows. There is also Néel-type finite-momentum triplet pairing between electrons 2 and 3, which is produced from electron 1 due to the Umklapp reflection process from the S/AF interface. The total momentum δp of the pair (2 and 3) is shown by the red arrow. The picture is adopted from Ref. [76].

From this dispersion relation and the condition that \( \varepsilon = 0 \) at the Fermi surface we obtain

The last expression can be rewritten in terms of the electron Fermi velocity \( v_{F,x} \equiv  v= \partial \varepsilon/\partial p_x = 2ta \sin (p_x a) \) at \( \mu_{AF}=h=0 \) as \( \delta p = 2\sqrt{\mu_{AF}^2 - h^2}/v \). The main contribution to the oscillations of the critical temperature is given by the normal trajectories with \( v_{F,x} \approx v_F \) and then the oscillation period takes the form

Figure 15 shows some typical examples of the spatial distribution of the on-site singlet and triplet correlations inside the AF layer at the \( A \)-sublattice. We see that the triplet correlations oscillate inside the antiferromagnet [the period of these oscillations is in agreement with Eq. (5)], while the singlet correlations just decay without oscillations, unlike the case of S/F heterostructures, where both singlet and triplet correlations manifest oscillations with the same period inside the ferromagnet. The reason is that according to our qualitative consideration only Néel pairs can have finite momentum of the described physical origin.

Figure 15

Dependence of the \( A \)-sublattice triplet correlations amplitude \( F_t \) (red curves) and the singlet amplitude \( F_s \) (blue curves) for the normal to the S/AF interface trajectory \( v > 0 \) on the distance from the S/AF interface inside the AF layer. Different curves correspond to different thicknesses \( d_{AF} \) of the AF layer. Each of the curves ends at the distance corresponding to the impenetrable edge of the AF layer. \( F_{s,0} \) is the singlet amplitude in the absence of the AF layer. The picture is adopted from Ref. [76].

Now we will discuss the effect which oscillations of the Néel triplet correlations have on the critical temperature of S/AF bilayers with metallic antiferromagnets. The sketch of the system is presented in Figure 16. In systems with finite-width layers these oscillating correlations can experience constructive or destructive interference due to the reflections from the impenetrable edge of the AF layer. This leads to the oscillating dependence of the Néel triplet correlations amplitude on the width \( d_{AF} \) of AF layer, what, in its turn, makes the critical temperature of the bilayer also an oscillating function of \( d_{AF} \).

Figure 16

S/AF bilayer with a finite-width metallic AF. Staggered magnetization of the AF layer is schematically depicted by arrows. The unit cell containing two sites belonging to \( A \) and \( B \) sublattices is also shown. The picture is adopted from Ref. [76].

Such behavior of the critical temperature was investigated in Ref. [76]. Figure 17-Figure 19 show the critical temperature as a function of \( d_{AF} \) for different values of the thickness \( d_S \) of the S layer. Different curves in each figure correspond to the different exchange fields \( h \) of the AF layer. In all three figures we can see the superconductivity suppression is accompanied by the oscillations of the critical temperature. The amplitude of the oscillations grows with the value of the exchange field, and its period is described well by Eq. (5) regardless of the thickness of the superconductor. As the S layer gets thinner, the influence of the proximity effect on the superconductor increases, which leads to a stronger suppression of the critical temperature and a larger amplitude of the oscillations. To see this we can compare Figure 17 and Figure 18. In Figure 18 corresponding to smaller \( d_{S} \) the amplitude of the oscillations is higher. This is because of larger amplitude of the triplet wave function reflected from the impenetrable edge of the AF. However, for the thinnest S layer (Figure 19) the \( T_c \) oscillations are weakly pronounced. This is explained by the fact that the amplitude of the oscillating Néel triplets inside the AF layer (and, consequently, the amplitude of the \( T_c \) oscillations) is greatly suppressed in this case together with superconductivity.

Figure 17

Critical temperature of the S/AF bilayer as a function of the AF layer thickness \( d_{AF} \), calculated for \( d_S=1.5\xi_S \). The picture is adopted from Ref. [76].

Figure 18

The same as Figure 17 but calculated for \( d_S=0.75\xi_S \). The picture is adopted from Ref. [76].

Figure 19

The same as Figure 17 but calculated for \( d_S=0.225\xi_S \). The picture is adopted from Ref. [76].

In this section we will discuss how Néel triplet correlations manifest themselves in AF/S/AF trilayers, following Ref.[78]. First of all, we need to define what the spin-valve effect is. Let us consider a heterostructure constructed of a superconductor and two magnetic layers. If the superconducting critical temperature of the hybrid structure is sensitive to the mutual orientation of the magnetizations of the magnetic layers, we call it a spin-valve effect and the structure can be referred as a spin valve. Switching between the superconducting and the normal states by changing the mutual orientation of the magnetizations is called the absolute spin-valve effect.

Spin-valve effect in heterostructures with ferromagnets has been widely studied theoretically[79-84] and experimentally[85-97],and its origin is intuitively clear. Indeed, let us introduce the misorientation angle φ between the magnetizations of the F-layers. Then in the parallel (P) configuration, corresponding to \( \phi=0 \), the exchange fields of the two F-layers strengthen each other, while in the antiparallel (AP) case with \( \phi=\pi \) they compensate each other. Therefore, we can expect that the critical temperature in the P case to be lower than in the AP case. However, is not always true because the interference of superconducting correlations makes the situation more complicated.

What happens with the spin-valve effect in AF/S/AF structure with fully compensated S/AF interfaces (i. e. with zero interface magnetization)? It may seem that such a system is invariant with respect to reversal of the direction of the Néel vector in one of the AF-layers. Then there would be no physical difference between parallel and antiparallel configurations and, consequently, no spin-valve effect. However, it was theoretically shown[98] that the superconducting spin-valve effect can be realized in AF/S/AF structures with insulating antiferromagnets and fully compensated S/AF interfaces despite the absence of macroscopic magnetization in the AF layers. The explanation is connected with the Néel triplet correlations generated by the two S/AF interfaces. Reversing the direction of the Néel vector in one of the AF-layers means reversing signs of the amplitudes of the Néel correlations generated by the corresponding S/AF interface. Therefore, these correlations, analogously to the exchange fields in spin valves with F-layers, can be added (subtracted) inside the superconducting layer depending on the misorientation angle between the Néel vectors, thus suppressing superconductivity more (less) strongly.

For describing the spin-valve effect in AF/S/AF systems with fully compensated interfaces it is convenient to define the misorientation angle \( \phi \) as it is shown in Figure 20. We perform a unified division of the entire AF/S/AF structure into two sublattices and define the misorientation angle as the angle between the magnetizations of two antiferromagnets at the same sublattice. Two following subsections are devoted to the influence of the chemical potential and impurities on the spin-valve effect in AF/S/AF structures with insulating antiferromagnets.

Figure 20

Sketch of the AF/S/AF system. Red and green arrows show Néel-type magnetizations of the AF-layers. The unified division into two sublattices with unit cells containing two sites belonging to \( A \) and \( B \) sublattices is also shown. The misorientation angle \( \phi \) is defined as the angle between the magnetizations of two antiferromagnets at the same sublattice. The picture is adopted from Ref. [78].

In this subsection we discuss the influence of the chemical potential \( \mu_S \) in the superconducting layer on the dependence \( T_c(\phi) \) in the clean case with no impurities in S. According to our definition of the misorientation angle, it seems reasonable to expect fulfillment of the relationship \( T_c^{P}<T_c^{AP} \) c [here \( T_c^P\equiv T_c(\phi=0) \) and \( T_c^{AP} \equiv T_c(\phi=\pi) \)], since in the parallel case the Néel triplets generated by the both S/AF interfaces are effectively summed up and strengthen each other inside the S-layer. However, as it will be clear from the following, away from half-filling (\( \mu_S=0 \)) the opposite result \( T_c^{P}>T_c^{AP} \) c can be realized depending on the width \( d_S \) of the S-layer.

At first we consider the \( T_c(\phi) \) dependence calculated in the case \( \mu_S=0 \) (Figure 21). We can observe that the spin-valve effect is well-pronounced and the relation \( T_c^P<T_c^{AP} \) c is fulfilled for all considered \( d_S \)values. For larger width of the S-layer the valve effect is reduced, which follows from physical considerations: in the limit \( d_S \gg \xi_S \) (\( \xi_S\approx 6 \) monolayers for the data presented in this subsection) the valve effect should disappear because the two S/AF interfaces do not feel each other and the superconductivity suppression at each of them does not depend on the direction of the Néel vector. The curve corresponding to \( d_S=6 \) monolayers demonstrates that for the system under consideration the absolute spin-valve effect, corresponding to the full suppression of superconducting state for a range of misorientation angles, can be realized.

Figure 21

Dependence of \( T_c \) on the misorientation angle \( \phi \) for the AF/S/AF structure at half-filling (\( \mu_S=0 \)). Different curves correspond to the different \( d_S \) values (all widths are measured in the number of monolayers). All calculations were performed for the following parameters: \( d_{AF}=4 \), \( \mu_{AF}=0 \), \( h=0.5t \), and \( T_{c0}=0.07 t \). The picture is adopted from Ref. [78].

Figure 22 corresponds to \( \mu_S=0.2 t \) and demonstrates that the relation between \( T_c^P \) and \( T_c^{AP} \) can depend on the \( d_S \) value. The reason is the finite-momentum Néel triplet correlations, discussed in Section 4. The amplitude of such correlations oscillates in the S layer with the period \( L_{\mathrm{osc}} = \pi v_F/|\mu_S| \). Depending on the width of the S layer the Néel triplets generated by the opposite S/AF interfaces can interfere constructively or destructively in the superconductor, which manifests itself in the oscillating behavior of the resulting Néel triplet amplitude for a given \( \phi \) upon varying \( d_S \). This physical picture is further supported by the demonstration of the dependence of \( T_c(0,\pi) \) on \( d_S \) presented in Figure 23. The oscillations of the difference \( T_c(\pi)-T_c(0) \) with the period \( L_{\mathrm{osc}} \), accompanied by changing sign of the spin-valve effect (i. e. the sign of \( T_c(\pi)-T_c(0) \), are clearly visible.

Figure 22

The same as Figure 21 but calculated for \( \mu_S=0.2 t \). The picture is adopted from Ref. [78].

Another interesting feature is the non-monotonous behavior of the \( T_c(\phi) \) dependence (Figure 22). The dip in the critical temperature at \( \phi \) close to \( \pi/2 \) can be explained by generating of so-called cross product correlations with the amplitude maximal at \( \phi \approx \pi/2 \). These are triplet correlations determined by \( \boldsymbol{h}_l \times \boldsymbol{h}_r \), where \( \boldsymbol{h}_{l,r} \) are the Néel vectors of the sublattice \( A \) of the left and right AFlayers, respectively, \( |\boldsymbol{h}_l|=|\boldsymbol{h}_r|=h \). These correlations are not of sign-changing Néel type and are usual equalspin triplet correlations. Its amplitude is equal to zero at \( \mu_S = 0 \), what explains an absense of the dips in Figure 21. In Figure 22 the dip can be clearly seen only for \( d_S=13 \) monolayers. For lower values of the S width the cross product correlations are too weak to result in the pronounced dip-like feature, as its amplitude is proportional to \( d_S/\xi_S \). For higher \( d_S \) values the influence of the cross product correlations is weakened due to a smaller overlap of the Néel triplet correlations generated by the opposite S/AF interfaces.

Figure 23

Dependences \( T_c(0) \) and \( T_c(\pi) \) as functions of \( d_S \) at \( \mu_S=0.9 t \). The calculations were performed for the following parameters: \( d_{AF}=4 \), \( \mu_{AF}=0 \), \( h=t \), and \( T_{c0}=0.03t \). The period of the oscillations is \( L_{\mathrm{ocs}} = \pi v_F/\mu_S \approx 7 \). Four periods (minima \( T_c(d_S) \) for \( \phi=\pi \)) are shown on the plot by vertical blue lines. The picture is adopted from Ref. [78].

It was shown[78, 98] that at \( h_{\mathrm{eff}}\equiv ha/d_S \ll T_c \) (here a is the lattice constant of the superconductor in the \( x \)-direction) the dependence \( T_c(\phi) \) takes the form \( T_c=T_{c,\parallel}+ \Delta T_{c,\parallel} \cos \phi + \Delta T_{c,\perp} \sin^2 \phi \), where \( T_{c,\parallel} = (T_c(0)+ T_c(\pi))/2 \), \( \Delta T_{c,\parallel} = (T_c(0)- T_c(\pi))/2 \) is the ”\( 0-\pi \)” spin-valve effect and \( \Delta T_{c,\perp}=T_c(\pi/2)-T_{c,\parallel} \) is the ”perpendicular” spin-valve effect, corresponding to the dips at the \( T_c(\phi) \) dependences at \( \phi=\pi/2 \). In this subsection we discuss the influence of impurities in the S layer on both ”\( 0-\pi \)” and ”perpendicular” spin-valve effects. The impurities are modelled as random changes of the chemical potential \( \mu_S \) at each site of the superconductor: \( \mu_i=\mu_S+\delta \mu_i, ~\delta \mu_i \in [-\delta\mu,\delta\mu] \), therefore the impurity strength is defined as δμ.

Figure 24 demonstrates the gradual disappearing of the ”\( 0-\pi \)” valve effect \( Delta T_{c,\parallel} \) under the influence of impurities. This is explained by the fact that the spin-valve effect of this type is produced by the Néel triplets, which appear due to interband electron pairing[34] and therefore are suppressed by impurities.

Figure 24

Suppression of the spin-valve effect by impurities. The difference \( \Delta T_{c,\parallel} \) is plotted as a function of the impurity strength \( \delta \mu \). The difference is normalized to its value at \( \delta \mu = 0 \). The dashed line is a guide for the eye. All calculations were performed for the following parameters: \( \mu_S=0.9\,t \), \( \mu_{AF}=0 \), \( h=t \), \( d_{AF}=4 \) and \( d_S=20 \) monolayers, and \( T_{c0}=0.03\,t \). The picture is adopted from Ref. [78].

Figure 25 presents the dependence of the ”perpendicular” spin-valve effect \( \Delta T_{c,\perp} \) on the impurity strength. We see that this effect tends to be insensitive to the presence of impurities. This can be considered as a proof of its origin from equal-spin cross product triplet correlations, which should be insensitive to impurities as they are conventional (not Néel) triplets and correspond to the intraband \( s \)-wave odd-frequency triplet electron pairing, which is not suppressed by nonmagnetic impurities.

Figure 25

The difference \( \Delta T_{c,\perp} \), normalized to its value at \( \delta \mu = 0 \) as a function of the impurity strength \( \delta \mu \). All parameters are the same as in Figure 24. The picture is adopted from Ref. [78].

It is well-known that the Andreev bound states can occur at single impurities in superconductors if the impurities suppress superconductivity for a given system[99]. In particular, magnetic impurities break the time-reversal symmetry and for this reason they are pair-breaking even for conventional \( s \)-wave superconductors. Well-known spinsplit Yu-Shiba-Rusinov states occur at magnetic impurities[100-102]. They attracted much attention over the last several decades[99], primarily due to the fact that on chains of magnetic impurities they can form topological bands due to overlapping of bound states at separate impurities[103-105].

It was recently demonstrated[77] that spin-splitted impurity-induced Andreev bound states can also occur in S/AF heterostructures with conventional intraband \( s \)-wave pairing at nonmagnetic impurities. The system considered in Ref.[99] is sketched in Figure 26 and represents a thin-film bilayer composed of a superconductor and a two-sublattice antiferromagnet. The general physical argument allowing for the bound state at a nonmagnetic impurity in such a system is that the impurity can be viewed as effectively magnetic, as it was already discussed in Section 3.2. The spin of a particular bound state is determined by the sublattice to which the impurity belongs, see Figure 26 for illustration.

Figure 26

Sketch of the S/AF bilayer with non-interacting impurities. Insulating two-sublattice antiferromagnet (AF) with staggered exchange field \( \boldsymbol{h}_A = -\boldsymbol{h}_B \) induces an effective staggered exchange field \( \boldsymbol{h}_{\mathrm{eff},A} = -\boldsymbol{h}_{\mathrm{eff},B} \equiv \boldsymbol{h}_{\mathrm{eff}} \) via the proximity effect in the adjacent thin superconductor (S). An impurity can occupy sites \( A \) or \( B \) in the S layer. Both possible variants are shown by red balls. LDOS of the Andreev bound states localized at the corresponding impurity is shown schematically. The energy spectrum of the bound states with the appropriate spin structure (red arrows) is also shown above the corresponding impurity. The picture is adopted from Ref. [77].

As it was shown in Ref.[77], the presence or absence of the Andreev bound states at single nonmagnetic impurities in S/AF bilayers is also very sensitive to the value of the chemical potential \( \mu \) of the superconductor. It is the third example of the remarkable sensitivity of the physics of S/AF heterostructures to the value of the chemical potential. For large values \( \mu \gg T_{c0} \), when the impurities can be viewed as effectively magnetic, the bound states exist. Energies of the bound states as functions of the impurity strength are plotted in Figure 27. It is seen that at stronger staggered effective exchange field \( h_{\mathrm{eff}} \) the bound state is shifted deeper inside the superconducting gap region. For comparison the energies of the Yu-Shiba-Rusinov bound states at a magnetic impurity with the same strength in a conventional \( s \)-wave superconducting host are plotted by the dashed lines. Unlike the case of magnetic impurity the nonmagnetic impurities in S/AF bilayers are not able to support low and zero-energy bound states. In this sense one can say that they are weaker pair-breakers as compared to the magnetic impurities. For small \( \mu \lesssim T_{c0} \) the bound states do not appear because the impurities are not effectively magnetic[77].

Figure 27

Dependence of the energies of the bound states as a function of the impurity strength \( U_0 \) normalized to the density of states \( N_F \) at the Fermi surface. Here \( \mu=20\Delta \) and \( \Delta \) is the value of the order parameter of the superconductor. The energy of the bound state \( \varepsilon_b \) is normalized to the value of the superconducting gap \( E_g^S \). Different colors correspond to the different \( h_{\mathrm{eff}} \) values. Dashed lines represent bound state energies at a magnetic impurity with the same strength in a conventional \( s \)-wave superconductor. The picture is adopted from Ref. [77].

The spatial region occupied by the bound state has a scale of the order of the superconducting coherence length \( \xi_S \). The exponential decay is superimposed by a powerlaw suppression analogously to the case of magnetic impurities in conventional superconductors[99]. However, unlike the magnetic impurities in conventional superconductors here the local density of states (LDOS) has a ”staggered” component, which oscillates between the sublattices. If the impurity is localized at \( A \)-site, the bound state LDOS is mainly concentrated at the \( B \)-sublattice everywhere except for the atomic-scale region near the impurity site. The spatial structure of the LDOS is shown in Figure 28.

Figure 28

Local density of states \( N \) at the energy corresponding to one of the bound states \( \varepsilon = -|\varepsilon_b| \) as a function of coordinates. The impurity is at \( A \)-site in the centre of the presented spatial region. The picture is adopted from Ref. [77].

An interesting feature of the spatial structure of the bound state LDOS is that the overall decay of the LDOS and the ”staggered” oscillations associated with the sublattice structure are also superimposed by oscillations of a larger spatial scale compared to the atomic one, which is nevertheless significantly smaller than the superconducting coherence length scale. These oscillations are due to the generation of finite-momentum Néel-type triplet correlations, which were discussed in Section 4. Here they are produced due to the Umklapp electron scattering processes at the impurities. The period of these oscillations is \( L_{\mathrm{osc}} = \pi v_F/ \sqrt{\mu^2 - h^2} \). Data presented in Figure 28 are calculated at \( h=1.5 t \) and \( \mu = 2 t \), giving us \( L_{\mathrm{osc}} \approx 4 a \), what is in agreement with the additional oscillation period seen in the figure.

The presence of the Andreev bound states at single nonmagnetic impurity in S/AF bilayers is in agreement with the behavior of the superconducting critical temperature of such systems in the presence of random disorder, which has already been studied[38] and discussed in Section 3. At \( \mu \lesssim T_{c0} \) the nonmagnetic impurities are not pair-breaking and they enhance superconductivity of S/AF bilayers due to the suppression of the Néel triplet correlations[34, 38]. On the contrary, if \( \mu \gg T_{c0} \) the superconductivity is suppressed by random nonmagnetic disorder[38, 17-19]. The same sensitivity to the value of the chemical potential occurs in the problem of a single impurity: the bound states only exist at \( \mu \gg T_{c0} \), when superconductivity is suppressed by impurities.

Many studies are devoted to the interplay of conventional correlations and spin-orbit coupling (SOC) in S/F hybrid structures[10, 106-112]. It was predicted and observed that SOC in S/F bilayers can produce an anisotropic depairing effect on triplets. One of the manifestations of the anisotropic depairing is that the critical temperature Tc of the bilayer depends on the orientation of the F layer magnetization with respect to the S/F interface[112-115]. This behavior is interesting not only from a fundamental point of view, but also for spintronics applications because there is a possibility for a reciprocal effect: reorientation of the F-layer magnetization due to superconductivity[116-118]. The possibility to control magnetic anisotropy using superconductivity is a key point in designing cryogenic magnetic memory and spintronics applications in near future.

In this section we discuss anisotropic effect of the Rashba SOC on the Néel triplets in S/AF thin-film bilayers. The key feature is that in addition to the anisotropic depairing of the triplet correlations known in S/F hybrids, a unique effect of anisotropic enhancement of the triplets by the SOC occurs in the S/AF case. We discuss the physical mechanism of the effect and demonstrate that it can manifest itself in opposite trend in the anisotropy of the superconducting transition as compared to S/F heterostructures. The SOC results in the depairing or enhancement of the Néel triplets depending on the value of the chemical potential of the superconductor and it is the fourth physical manifestation of the strong sensitivity of the physics of S/AF hybrid structures to the value of the chemical potential.

The anisotropic effect of the Rashba SOC was considered in Ref. [119] by an example of a thin-film S/AF bilayer, where the antiferromagnet is assumed to be an insulator (Figure 29). The SOC is induced in the S layer by proximity to a heavy metal layer like Pt (shown as the SO layer in Figure 29). The SOC can also be due to the inversionsymmetry breaking in the S film by itself. The magnetism is staggered. The S/AF interfaces were assumed fully compensated (i. e., the interface magnetization has zero average value). The influence of the antiferromagnetic insulator on the superconductor was described by the exchange field \( \boldsymbol{h}_{\mathrm{eff},\boldsymbol{i}} = \boldsymbol{(-1)}^{i_x+i_z} \boldsymbol{h}_{\mathrm{eff}} \).

Figure 29

Sketch of the thin-film S/AF bilayer with SOC. The Néel vector of the AF makes angle \( \theta \) with the plane of the structure. \( \theta=0 \) corresponds to the in-plane (IP) and \( \theta=\pi/2 \) accounts for the out-of-plane (OOP) orientations. Unit cell with two sites \( A \) and \( B \) is also shown. The picture is adopted from Ref. [119]

Figure 30 shows the dependences T\( T_c(h_{\mathrm{eff}}) \) for S/AF structures with in-plane (IP) and out-of-plane (OOP) orientations of the Néel vector. They have been compared to \( T_c(h_{\mathrm{eff}}) \) of the S/F system with the same absolute value of the effective exchange field \( h_{\mathrm{eff}} \) (conventional, not staggered). First, it is seen that while for S/F heterostructures \( T_c \) is always higher in the presence of SOC (dashed curves), for S/AF heterostructures the trends are opposite for large \( \mu \gg T_{c0} \) and small \( \mu \lesssim T_{c0} \). At small \( \mu \) the behavior of \( T_c \) is qualitatively similar to the case of S/F bilayers, and at large \( \mu \) it is opposite: the presence of SOC suppresses \( T_c \).

Figure 30

a, b – Critical temperature of S/AF (solid curves) and S/F bilayers (dashed) as a function of the effective exchange field \( h_{\mathrm{eff}} \). Panels a and b correspond to \( \mu=12 T_{c0} \) and \( \mu=0 \), respectively. Green curves represent the results with no SOC, red and blue curves are for out-of-plane (OOP) and in-plane (IP) orientations, respectively, and \( V_R = 0.4t \) is the Rashba SOC strength. The picture is adopted from Ref. [119].

Furthermore, in the presence of SOC \( T_c \) becomes anisotropic and it depends on the angle \( \theta \) between the magnetization and the interface plane. For S/F heterostructures Tc is always higher for the OOP orientation (dashed curves)[112-115]. At the same time for S/AF heterostructures the ratio between the values of Tc for both IP and OOP orientations is again opposite for large \( \mu \gg T_{c0} \) and small \( \mu \lesssim T_{c0} \). At \( \mu \lesssim T_{c0} \) for S/AF heterostructures the ratio between \( T_c \) for both IP and OPP orientations is the same as for the S/F case. At \( \mu \gg T_{c0} \) the anisotropy of the critical temperature (in the other words, the difference between \( T_c \) for the IP and OOP orientations) is opposite.

Here we discuss the physical reasons of the numerical findings described in the previous subsection. First of all, as it was already discussed in Section 2.5, if \( \mu \lesssim \pi T_{c0} \), then the most important contribution to the pairing correlations is given by the electronic states corresponding to \( \xi_\pm \approx 0 \). This means that the electrons are at the edge of the antiferromagnetic gap and, therefore, practically fully localized at one of the sublattices. Consequently, they only feel the magnetization of the corresponding sublattice and behave in the same way as in the ferromagnet. For this reason our results at \( \mu \lesssim \pi T_c \) demonstrate the same trends as the corresponding results for S/F structures. It is well-known that in S/F heterostructures the critical temperature is higher for OOP magnetization orientation than for the IP magnetization[115] due to the fact that SOC suppresses triplets oriented OOP more than triplets oriented IP. The same is observed in Figure 30b for S/AF bilayers with \( \mu=0 \). Moreover, the SOC always suppresses triplets and, correspondingly, enhances \( T_c \). The same is seen in Figure 30b for S/AF heterostructures.

Figure 30

a, b – Critical temperature of S/AF (solid curves) and S/F bilayers (dashed) as a function of the effective exchange field \( h_{\mathrm{eff}} \). Panels a and b correspond to \( \mu=12 T_{c0} \) and \( \mu=0 \), respectively. Green curves represent the results with no SOC, red and blue curves are for out-of-plane (OOP) and in-plane (IP) orientations, respectively, and \( V_R = 0.4t \) is the Rashba SOC strength. The picture is adopted from Ref. [119].

The opposite trend at \( \mu \gg T_{c0} \) is due to the existence of a unique mechanism of generation of the Néel triplet correlations in S/AF heterostructures, which differs from the mechanism of the direct singlet-triplet conversion known in S/F heterostructures. The Néel triplets are generated via the normal state Néel-type spin polarization of the DOS[119]. Up to the leading order in \( h_{\mathrm{eff}}/|\mu| \) and \( h_R/|\mu| \) the Néel-type polarization of the normal state DOS along \( \boldsymbol{h}_{\mathrm{eff}} \) and at the Fermi surface takes the form

where \( N_F \) is the normal-state DOS at the Fermi surface of the isolated superconductor, \( \boldsymbol{h}_R \propto V_R (\boldsymbol{e}_y \times \boldsymbol{v}_F) \) is the effective Rashba pseudomagnetic field acting on an electron moving along the trajectory determined by the Fermi velocity \( \boldsymbol{v}_F \) and \( \phi \) is the angle between \( \boldsymbol{h}_{\mathrm{eff}} \) and \( \boldsymbol{h}_R \). It is seen that (i) the absolute value of the polarization is always enhanced by the SOC and (ii) the enhancement is anisotropic. It reaches maximal possible value for all the trajectories for out-of-plane orientation of \( \boldsymbol{h}_{\mathrm{eff}} \) because \( \boldsymbol{h}_R \) is always in-plane. The reason for the described above enhancement is the specific reconstruction of normal state electron spectra under the influence of the SOC[119].

In S/F heterostructures the effective exchange field \( \boldsymbol{h}_{\mathrm{eff}} \) is also generated in the superconductor due to proximity with a ferromagnetic insulator. It results in the occurrence of the normal state polarization of the DOS of conventional type \( P \sim N_F (h_{\mathrm{eff}}/\varepsilon_F) \ll N_F \). However, this polarization is always very small, because the effective exchange induced in the superconductor cannot be higher than the superconducting order parameter[9], otherwise it completely suppresses superconductivity. Therefore, in S/F bilayers this quantity does not play a significant role in the generation of triplets. At the same time, the Néel type polarization, described by Eq. (6) is not necessary small and provides a generator for the Néel triplets. The enhancement of the Néel type polarization of the normal state by SOC leads to the enhancement of the Néel-type triplet correlations in S/AF structures. It was obtained in Ref.[119] that at \( \mu \gg T_{c0} \) up to the leading order in \( h_{\mathrm{eff}}/|\mu| \) \( h_R/|\mu| \) the anomalous Green’s function of the Néel-type triplet correlations takes the form:

where \( \omega \) is the Matsubara frequency. The component of \( \boldsymbol{f}^y \) along the effective exchange field \( \boldsymbol{h}_{\mathrm{eff}} \), which accounts for the suppression of the critical temperature by the triplets, takes the form:

Thus, the amplitude of the Néel triplet correlations qualitatively follows the normal state Néel polarization and it is also enhanced by the SOC. The effect of the enhancement is the strongest for the OOP orientation corresponding to \( \phi = \pi/2 \).

In this review we discussed the physics of Néel triplet proximity effect in S/AF heterostructures, which was studied in a number of recent papers. The main findings can be summarized as follows:

1. At S/AF interfaces unconventional triplet correlations are generated. The amplitude of the corresponding pair wave function flips sign from one site of the materials to the nearest one following the Néel structure of the antiferromagnetic order parameter. The correlations can occur in superconductors due to proximity to the antiferromagnetic insulators and metals and penetrate into antiferromagnetic metals from superconductors. They are generated even at fully compensated S/AF interfaces with zero net magnetization of the interface. These triplet correlations were called the Néel triplet correlations.

2. The Néel triplets suppress superconductivity. The efficiency of the suppression is of the same order and frequently a bit stronger than the suppression by the conventional proximity-induced triplet correlations in S/F heterostructures.

3. The mechanism of the Néel triplets generation differs from the well-known direct singlet-triplet conversion in S/F heterostructures. They are produced via the effect caused on the singlet superconducting correlations by the Néel-type normal state electron polarization, induced in the superconductor by proximity to the AF. This mechanism results in the opposite as compared to S/F heterostructures trends in the anisotropy of the critical temperature of S/AF heterostructures in the presence of SOC.

4. The higher the Néel exchange field of the AF or proximity-induced effective exchange field in the S the stronger the amplitude of the Néel triplets, is. At the same time, unlike S/F heterostuctures the amplitude of the Néel triplet correlations is very sensitive to the value of the chemical potential in the material, where they are induced. Deviation from half filling suppresses the amplitude of the Néel triplets for a given value of the Néel exchange field.

5. Near half-filling the Néel triplets are interband, and far from half-filling they are intraband. It results in very different response of the Néel triplet correlations on the nonmagnetic impurities: near halffilling the Néel triplets are suppressed by impurities and far from half-filling they are immune to impurities.

6. The above behavior of the Néel triplets in the presence of nonmagnetic impurities leads to very different dependencies of the critical temperature of S/AF bilayers on the impurity strength: near halffilling the impurities enhance the critical temperature, and far from half-filling they suppress it. The second tendency is caused by an additional mechanism: far from half-filling the nonmagnetic impurities in S/AF heterostructures behave like effectively magnetic and suppress singlet superconductivity by themselves.

7. The effective magnetic character of the nonmagnetic impurities in S/AF heterostructures leads to the occurrence of the spin-split Andreev bound states at single impurities, which are reminiscent of wellknown Yu-Shiba-Rusinov bound states at magnetic impurities in superconducting materials, but occurring at nonmagnetic impurities.

8. The Néel triplet correlations provide a possibility to realize a spin-valve effect in AF/S/AF trilayers even with fully compensated interfaces.

9. Due to the lost of the translational invariance at S/AF interfaces and/or at single nonmagnetic impurity a finite-momentum Néel triplet pairing can occur. It results in (i) the oscillations of the critical temperature of S/AF bilayers with metallic antiferromagnets as a function of the thickness of the AF layer, (ii) peculiar oscillations of the impurityinduced DOS around nonmagnetic impurities, and (iii) sign inversion of the spin-valve effect in AF/S/AF trilayers upon varying the width of the S layer.

10. Unlike S/F heterostructures the physics of S/AF heterostructures is crucially sensitive to the value of the chemical potential. Two physically very different regimes can be identified near half-filling and far from half-filling. In particular, the dependence of the critical temperature of S/AF heterostructures on impurity concentration is opposite in these regimes, the dependence of the critical temperature of heterostructures with canted AFs on the canting angle is also opposite, the same applies to the magnetic anisotropy in S/AF heterostructures with SOC and to the formation of the Andreev bound states at single nonmagnetic impurities.

It could be especially interesting to study the described effects in heterostructures composed of antiferromagnets and 2D superconductors because of possibility of external control of the chemical potential.

We are grateful to A. A. Golubov for the discussion of the obtained results. The work was supported by Russian Science Foundation (project No. 23-72-30004.)

Corresponding author: Irina V. Bobkova, https://orcid.org/0000-0003-1469-1861, e-mail ivbobkova@mail.ru.

The authors declare no competing financial or non-financial interests.